Inscription / Connexion Nouveau Sujet
algebra 1
Salut, j'ai besoin de votre aide avec cette expression algébrique.
J'ai pensé à distribuer le 2 et le 6.
trouver les termes semblables et simplifier.
J'ai obtenu y =6 comme résultat, mais ce n'est pas correct.
Le choix multiple ne contient que des ensembles de nombres comme {2,3}, {-3,-3} ,{-3,3}.
quoi faire?
Merci beaucoup!
Bonjour,
une expression, .. ou une équation ??
règle absolue ici :
recopier mot à mot son énoncé et pas le raconter de travers à sa sauce.
(et puis quand on a des doutes sur ses calculs on les recopie en entier)
"trouver y " ça veut dire résoudre une équation,pas simplifier une expression !
pour résoudre cette équation il n'y a rien à simplifier du tout
et certainement pas les trucs archi faux que tu as fait
mais utiliser :
"un produit est nul si un des facteurs est nul". terminé.
un produit est nul si un des facteurs est nul". terminé.
pourriez-vous recommander un tutoriel.
Je ne veux pas que l'équation soit résolue pour moi. Je veux de l'aide pour la mener à une solution.
L'aide peut prendre la forme de conseils, d'indices ou de tutoriels, comme Lelie l'a toujours fait avec moi.
vous me dites que je devrais résoudre
en utilisant la propriété du produit nul, c'est ca?. ok, je vais tenter le coup et voir. si je suis bloqué, aide-moi s'il te plaît.
dans ![]() cours puis exercices d'application sur la résolution d'équations
cours puis exercices d'application sur la résolution d'équations
il n'y a rien de plus que ce que j'ai dit. toutefois tu y trouveras un exercice résolu : l'exercice 2
résoudre (2x + 1)(x - 4) = 0
quasiment identique au tien pour la méthode à appliquer.
.
C'est l'équation que tu (mathafou) m'as donné à résoudre.
Je résoudrai celle du fil demain.
Désolé d'être en retard. j'ai eu fort à faire.
et
ensemble de solutions
Qu'en penses-tu?. Ces't correct?. Merci
Bonjour,
en attendant le retour de mathafou :
résoudre (2x + 1)(x - 4) = 0
les solutions sont en effet x = -1/2 et x=4
à présent, tu peux revenir à ton exercice
2(y-3)* 6(-y-3)=0
à toi !
bonjour,
C'est l'équation que tu (mathafou) m'as donné à résoudre.
Uniquement dans le but de préciser de quel "exercice 2" je parlais comme exemple
tu l'as refait toi même, c'est bien (c'est toujours préférable de refaire soi-même plutôt que de simplement lire le corrigé en croyant que ça suffit à le comprendre)
de là à le recopier ici ....

oui, mais il y a un peu plus simple :
il y a quatre facteurs
2, y-3, 6 et -y-3
2 et 6 ne sont pas nuls (!!)
reste uniquement à considérer y-3 et -y-3 qui peuvent être nuls et directement les deux solutions.
sans besoin de développer pour rediviser après par 2 et par 6 ! totalement inutile
l'exo est donc terminé
par contre je me dois de revenir sur le premier message
car c'est l'indice d'erreurs grave, très graves :
distribuer le 2 et le 6.
trouver les termes semblables et simplifier.
mais l'application que tu en as faite qui est complètement erronée (grave)
le fait que tu trouves à la fin "y = 6" est l'indice d'erreurs extrêmement graves :
tu confonds sommes et produits
et "trouver les termes semblables", certes mais certainement pas n'importe où et n'importe comment.
montre les calculs que tu avais fait pour que je t'indique précisément les erreurs.
(ce que je te demandais déja dès ma première réponse)
tu dis> oui, mais il y a un peu plus simple :
ça me plaît beaucoup .Merci.
Tu veux que je refasse ce qui m'a conduit à y=-6?
ok. C'est bon, on y va!.
Mais maintenant je sais que la propriété du produit nul peut être utilisée pour résoudre des équations comme celles-ci.
2(y-3)*(6(-y-3)
2y-6-6y-18=0-4y-24=0 faux dès cet instant.
correct est :
(2y-6) multiplié par (-6y-18)
(2y-6)(-6y-18)
c'est bien ce que j'avais pensé : tu confonds les sommes et les produits.
et si on veut aller plus loin dans ce développement on doit (produit de deux sommes) appliquer la double distribution ;
extrait du cours ![]() Calcul littéral :
Calcul littéral :
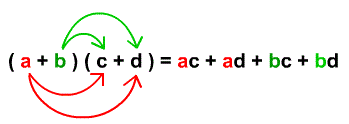
ici cela donnerait
(2y-6)(-6y-18) = (2y)*(-6y) + (2y)*(-18) - 6*(-6y) - 6*(-18)
= -12y² - 36y + 36 y + 108 (en appliquant la règle des signes dans les différents produits)
= -12y² + 108 (en regroupant - 36y + 36 y)


 en troisième
en troisième