Inscription / Connexion Nouveau Sujet
probléme en maths
Bonjour, j'ai un problème à résoudre en maths.
En effet Alexandre et Clément aiment les boissons énergétiques. Ils ont proposé aux leurs camarades lors d'une soirée à boire du « redbull » et du « monster ». Ils ont procuré du « redbull » à 4.8 dollars et du « monster » à 3.6 dollars. Ils ont claqué en tout 60 dollars et ils ont consommé tous deux boissons énergétiques. Combien des camarades ont consommé des boissons énergétiques ?
Je ne sais pas comment le resoudre, j'ai essayé mais j'ai pas trouvé une piste .
Bonsoir
le nombre de redbull
de monster
écrivez la relation et cherchez les points à coordonnées entières appartenant à la droite
non
est l'équation cartésienne d'une droite.
Tous les points de cette droite vérifient la relation.
On s'intéresse seulement aux points de la droite à coordonnées entières ,
puisque cela doit être le nombre de canettes de chaque sorte achetées.
Donc j'ai fait ça :
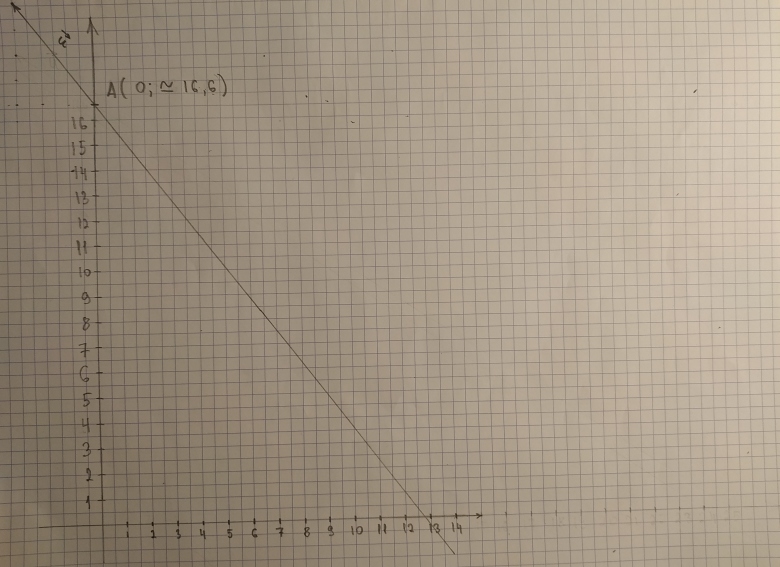
4x+3y = 50
a = 4, b = 3, le vecteur (-3;4) est un vecteur directeur de la droite d.
x=0
4*0+3y=50
3y=50
y=50/3 = environ 16,6
Donc A (0;environ 16,6)
Vous pouvez m'expliquer s'il vous plait comment je continue ?
On cherche les points à coordonnées entières
Apparemment (2; 14) répond à la question en effet
Maintenant comme vous l'avez écrit est un vecteur directeur de la droite
ainsi cela fait remonter dans les abscisses donc on va lui préférer
le deuxième point satisfaisant est
On continue tant que l'on reste dans le premier quadrant.
Comme chaque participant boit 2 canettes le nombre doit être pair
On a deux réponses possibles
2+14=16 donc 8 personnes eux 2 plus 6 camarades
ou 8+6=14 donc 7 personnes + 5 camarades
Rien pour départager
Juste encore une question pour être sûr. Si par exemple on change les prix ; c'est-à-dire 2,40 dollars pour « redbull » et 1,80 dollars pour « monster » et la somme totale claqué est 30 dollars.On va avoir le même raisonnement ?
2,40 x + 1,80 y = 30
2x + 1,5y = 25 ( on a simplifié tout par 1,2)
a = 2 ; b = 1,5, le vecteur a pour coordonnées (-1,5 ; 2)
x=0
2*0+1,5y=25
y = environ 16,7
On trace le système orthonormée est on trouve la même chose , c'est-à-dire 8 e 7.
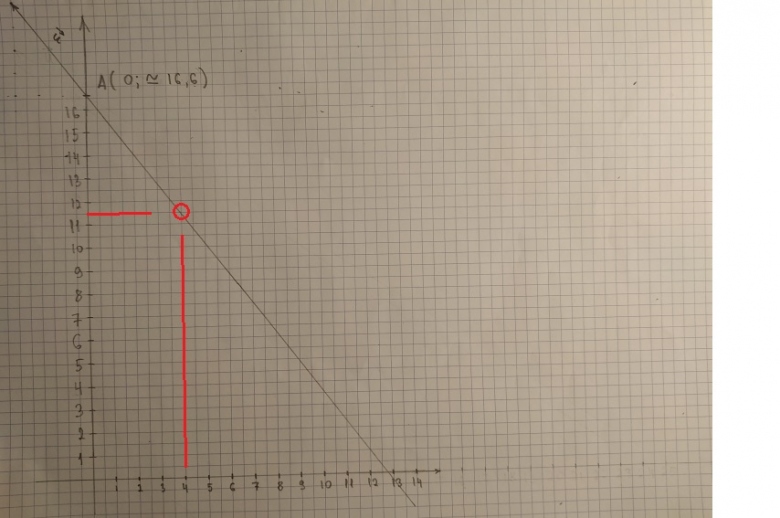
Et encore une question, si tous les points de cette droite vérifient la relation, pourquoi quand on choisit dans le premier cas par exemple le couple (4 ;11.5) et on calcule : 4*4+3*11.5, le résultat est 50.5 ?
Il ne doit pas être 50 ? C'est moi qui a tracé mal la droite ou c'est normal ?
Bonjour,
une lecture graphique est forcément une approximation
et le tracé d'une droite en prenant 16,6 comme "valeur" de 50/3 aussi.
pour tracer de façon précise la droite il est indispensable de tracer des points exacts et pas des approximations décimales au départ !
...des points à coordonnées entières par exemple ! 
c'est à dire de résoudre le problème pour tracer la droite et pas le contraire ...
dans ton exemple tu as mal lu (de façon imprécise) le point de ta droite :
même sur ce graphique on voit que le point (4; 11.5) est au dessus de la droite
Un méthode pas trop compliquée pour résoudre de façon algébrique (par le calcul) le problème, autrement que par l'approximation d'une lecture graphique.
4x+3y = 50
peut s'écrire
3(x+y) + x = 3*16 + 2
et on est amené à résoudre le système
x+y = 16
x = 2
une fois qu'on a obtenu ainsi une solution, on obtient toutes les autres en ajoutant ou retranchant le vecteur directeur (interprétation graphique, pas tracé graphique) entier le plus simple, qui est ici (3; -4)
et en se limitant au domaine du problème (x et y >0)
PS :
** ...au domaine du problème (x et y >0 et x+y pair) **
j'allais oublier la deuxième condition de l'énoncé
On va dire qu'on a resolu le système x+y = 16 et on a trouvé les points (2;14).
x = 2.
Si on ajoute : 2+3=5 on trouve (5;11) et du coup 4*5+3*11=53
14+(-3)=11
l'application du vecteur (3; -4) consiste à ajouter 3 à x et à retrancher 4 à y !!
2+3 = 5
14 -4 = 10
4*5 + 3*10 = 50
ce qui est bien une solution de 4x + 3y= 50
mais n'est pas solution du problème car x + y = 15 est impair
si on ajoute une deuxième fois ce vecteur directeur :
5 + 3 = 8
10 - 4 = 6
on trouve la deuxième solution déja connue (8; 6)
(vérification 4*8 + 3*6 = 50)
etc.
(puis (11, 2) rejetée car somme impaire
puis (14; -2) et les suivantes rejetées car y <0)



