Bonjour.

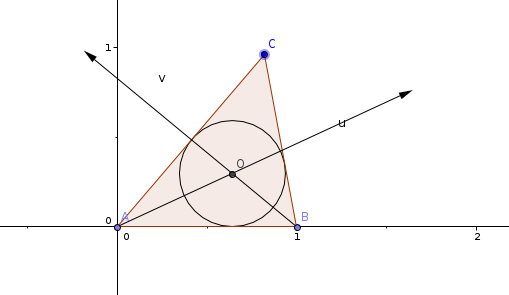
ABC est un triangle. On se place dans le repère (A, i, j) orthonormée. On a :
A(0,0)
B(1,0)
C(,), 0

Déterminer les coordonnées de O le centre du cercle inscrit.

----------------------------------------------------------------------------------------------------------------
Je rappelle que O est également l'intersection des bissectrices du triangle ABC.
Donc voici comment j'ai eu l'idée de procéder :

Je calcule = vAB + vAC, qui est un vecteur directeur de la bissectrice issue du sommet A.
Je calcule = vBA + vBC, qui est un vecteur directeur de la bissectrice issue du sommet B.

Je détermine l'équation cartésienne de la droite D1(A,)
Je détermine l'équation cartésienne de la droite D2(B,)

Je détermine le point d'intersection de D1 et D2 qui n'est autre que O.


Je trouve
X_O = (+1)/3
Y_O = /3

Cependant d'après la correction, ce n'est pas le bon résultat (je crois que eux ils le font en utilisant la formule de la distance du point aux droites (AB), (BC), (CB)).

Merci d'avance.