J'aurai voulu savoir aussi comment montrer que cet ensemble est connexe mais non connexe par arcs.

Je me suis trompé, en fait pour la connexité, c'est l'ensemble que je cherche à voir si il est connexe et non connexe par arcs.

Bonjour

Il n'est pas connexe par arc, mais il est connexe. Pour montrer cela, il faut démontre qu'il est "bien enchaîné".

Il me semble compact comme "fermé dans un compact". Il est fermé puisque c'est une adhérence.

Sauf erreur.

Bonjour jeanseb,

merci, en fait c'était l'ensemble de mon premier post que je voulais savoir si il était compact ou pas.
Mais bon il ne serait pas compact car pas fermé, étant donné que tu me dis que l'ensemble de mon post de 13:40 est son adhérence, si j'ai bien compris.

On va noter pour s'y retrouver:

,



donc pour montrer que est connexe, je montre qu'il est bien enchaîné sachant qu'il est compact ok. Mais comment je montre que cet ensemble n'est pas connexe par arcs?

Le premier ensemble n'est pas fermé car les points ak(1/k;0)forment une suite d'elements de cet ensemble, qui tend vers l'origine, extérieure à l'ensemble. Donc, effectivement, pas fermé.

Pour "non connexe par arcs", je ne vois pas directement comment raisonner.

Salut à tous

Pour la non connexité par arcs, je propose une idée comme ça : supposer par l'absurde que l'on puisse relier le point au point (0,0) par un arc continue (notons f une fonction continue sur [0,1] telle que et f(1)=(0,0)).

Notons a la borne inférieure de l'ensemble des t tel que f(t) appartienne au segment vertical : montrer qu'elle existe ,que f(a)=(0,0) et donc que a > 0.

Remarquer alors que pour t < a, f(t) n'appartient pas au segment vertical.
essayer d'aboutir à une contradiction.

Kaiser

Bonjour

D'abord T est connexe car c'est l'adhérence de S qui l'est évidemment.

Soit f:[0,1]T continue telle que f(0)T\S et f(1)S. On pose f=(f₁,f₂). Alors f₁(0)=0 et f₁(1)>0.
Soit a=sup{t[0,1] | f₁(a)=0}. A cause de la continuité, a<1 et f₁(a)=0. Mais pour t>a on a alors f(t)S donc
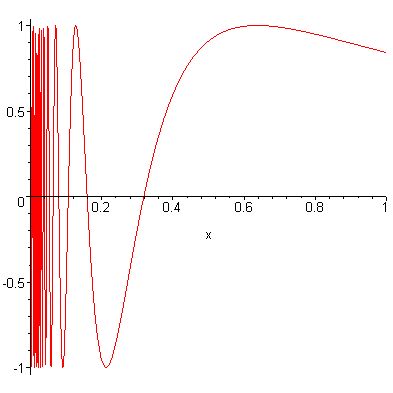
Mais si t tend vers a par valeurs supérieures f₁(t) tend vers f₁(a)=0 et sin(1/f₁(t)) aurait une limite. Or on sait que ceci est faux!

Bonjour,

Salut à tous

blang > effectivement, je me suis gourré !

Kaiser

>kaiser Oui, mais c'est la bonne idée!

Bonjour Camélia et Kaiser

Non seulement vous êtes bons, mais en plus vous êtes rapides!

Salut jeanseb

Ce n'est pas la première fois que je vois ce truc! Si ce genre de choses t'amuse, regarde ça: PEIGNES et topologie

merci, je vais regarder ça.

Bonjour,

j'ai trouvé un exo qui a l'air de proposer un plan différent pour montrer la non connexité par arcs de (cf mon post du 04/03/2008 à 14:20):

Citation :
1. Soit continue telle que . Montrer que l'ensemble est ouvert et fermé.

2. En déduire que n'est pas connexe par arcs.