Annuler
connectez vous
analyse complexe en post-bac
- Les nombres complexes - supérieur
- Nombres complexes : les classiques
- Équations différentielles : un Cours complet avec des exemples
- Ensemble et application Partie II
- Généralités sur les matrices, applications linéaires, changement de base, rang d'une matrice - supérieur
- Espaces vectoriels et Applications linéaires - supérieur
- Ensemble et application Partie I
Inscription / Connexion Nouveau Sujet
Accueil l'île des mathématiques Forum de mathématiquesListe de tous les forums de mathématiques SupérieurOn parle exclusivement de maths, pour le supérieur principalement, les BTS, IUT, prépas... Maths sup Analyse complexeTopics traitant de analyse complexe [tout]Lister tous les topics de mathématiques
Niveau Maths sup
Exercice sur les complexes
Posté par mario75
Bonjour,
Je suis bloqué à la question 2 de cet exercice :
1.Resoudre dans C l'equation E:z^7=1
Comme on le fait dans l'a fait dans le cours, j'ai bien trouvé 7 solutions différentes.
On note desormais omega(w) l'une des solutions de E différente de 1
2.Calculer S1=1+w+w²+w^3+w^4+w^5+w^6
Je suis parti de exp[(i*2k*pi)/7]
Puis ,j'ai montré que celà revenait à calculer la somme des 7 premiers termes d'une suite géométrique de premier terme 1 et de raison q=exp[(i*2k*pi)/7]
Et j'arrive à : S1=(1-exp[(i*2k*pi)/7]^7) / (1- exp[(i*2k*pi)/7] )
Mais je n'arrive pas à continuer ce calcul
Suis-je sur la bonne voie, ou mon raisonnement est-il faux ?
Merci de m'aider 
C'est très bien jusque là, il reste à remarquer que d'après la question 1, on a 1-w^7=... (où w=exp[(2ik*pi)/7]
C'est justement là que je bloque; je trouve que :
w7 =1
Celà reviendrait donc à ce que S1=0
Mais j'ai l'impression de me tromper en calculant w7
Est-ce que c'est correct ?
Oui c'est exactement ça! Je ne suis pas doué avec Latex mais ça se voit sur un dessin (on "tourne de 2pi/7 sur le cercle unité, si on trace les points on "voit" que ça fait zéro)
Merci beaucoup de m'avoir guidé !
( je doutais, car deux personnes de ma classe m'ont soutenu que la solution était S1 = 1, ce qui m'a mis dans le doute 
Ensuite, je dois calculer :
S2=w/(1+w2) + w2/(1+w4) + w3/(1+w6)
Donc, j'ai encore une fois, remplacé w par exp[(2ik*pi)/7], et j'ai appliqué la formule : (ex)n
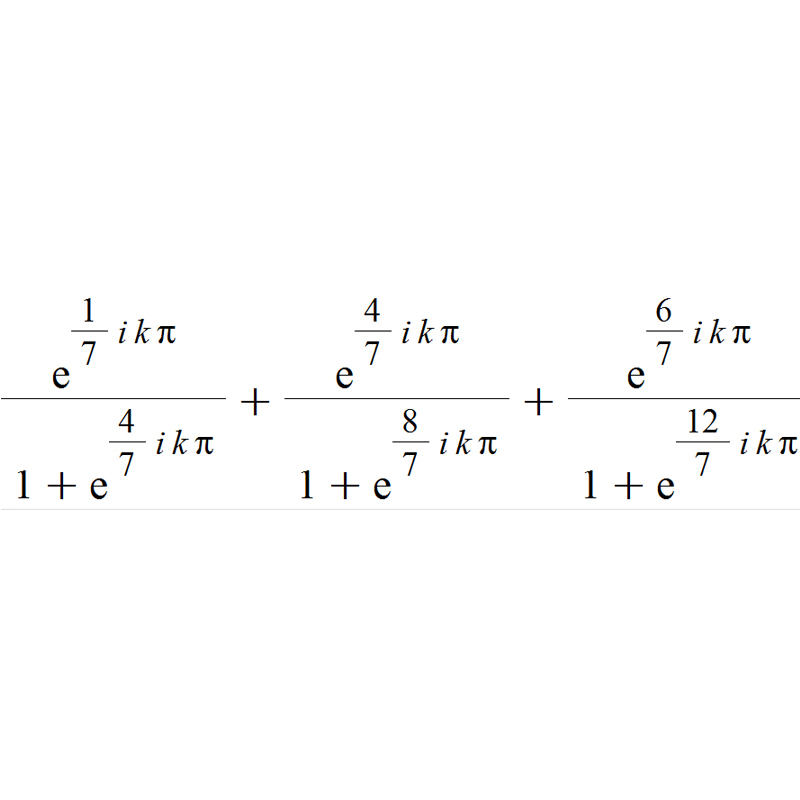
Avec ça, j'obtiens trois fractions, additionnées, mais où je suis bloqué ( je ne sais pas me servir de Latex, alors je vais scanner mon brouillon pour vous montrer )
J'ai fait ce qu'il fallait faire ?
Voilà ce que j'obtiens pour S2 ( regardez l'image attachée; comme je ne sais pas me servir de Latex, j'ai tapé ce que j'obtiens sur Maple ).
C'est correct pour l'instant ?
Je n'ai pas le fait le calcul, mais à mon avis si tu mets tout au même dénominateur tu auras une très joli surprise (MAIS GARDE LES w !!!)
(Une petite astuce : w8=w^7*w=1*w=w, w^9=w² et w^10=w^3, ça devrait servir pour conclure)
J'obtiens une trèèèèès longue fraction, avec toute une série de w+w2+w3+.....
Normalement, je devrais tomber sur quelque chose de court et simple ?
Tu obteins effectivement un truc très long, et d'après la question 1, il y a plein de trucs qui font zéro...
Je n'arrive pas à simplifier par le résultat de la question 1; il manque certaines valeurs, comme w3 par exemple.
Comment dois-je faire ?
Je n'arrive pas à obtenir w6 au numérateur.
Au dénominateur, j'ai bien réussi la simplification, en transformant w8 en w, w9 en w2, etc...
Mais au numérateur, je n'ai ni w6, ni w12, qui me permettraitd'obtenir w6 pour simplifier par la question précédente.
Comment dois-je faire pour pouvoir simplifier davantage ?
OK, je vais refaire le calcul.
Moi, au dénominateur, je trouve w6, donc ça voudrait dire que : S3=-2
Je comptais refaire le calcul par moi-même 
Ce que je ne comprends pas, c'est que je n'obtiens, qu'au maximum et au numérateur, w5.
Il me faudrait w6 pour pouvoir simplifier par la question 1, mais je n'arrive pas à le faire "apparaitre".COmment dois-je faire ?
Ah oui !!
J'avais complètement zappé ça, donc, j'otiens bien à présent -2w6 au numérateur
Merci !
A présent, je dois en déduire la valeur de S3=1/cos(2pi/7) + 1/cos(4pi/7) + 1/cos(6pi/7)
J'imagine que la question précédente va nous aider, non ?