Annuler
connectez vous
analyse complexe en post-bac
- Les nombres complexes - supérieur
- Nombres complexes : les classiques
- Ensemble et application Partie II
- Équations différentielles : un Cours complet avec des exemples
- Généralités sur les matrices, applications linéaires, changement de base, rang d'une matrice - supérieur
- Espaces vectoriels et Applications linéaires - supérieur
- Ensemble et application Partie I
Inscription / Connexion Nouveau Sujet
Accueil l'île des mathématiques Forum de mathématiquesListe de tous les forums de mathématiques SupérieurOn parle exclusivement de maths, pour le supérieur principalement, les BTS, IUT, prépas... Licence Maths 1e ann Analyse complexeTopics traitant de analyse complexe [tout]Lister tous les topics de mathématiques
Niveau Licence Maths 1e ann
Factorisation dans IR
Posté par tobi
Bonjour à tous, j'ai besoin d'être pour un exercice, je n'ai pas très bien compris la méthode que le prof nous a donné dans la correction.
Je dois factoriser l'expression suivante dans IR :
P(z) = −z3 + z2 + 2z + 12 en sachant que -1+i
3 est une racine.
Je sais que -1-i3 est aussi une racine.
Bonjour,
La somme des deux racines:
Le produit des deux racines:
Le polynôme est donc factorisable par
Bonsoir,
si -1+isqrt(3) et son conjugé sont des racines, alors dans C le polynome peut se factoriser sous la forme a(z-b)(z+1-isqrt(3))(z+1+isqrt(3)).
Du coup en développant : q(z)=(z+1-isqrt(3))(z+1+isqrt(3)) tu obtiens un trinome à coefficients réels, et alors tu auras P(z)=a(z-b)q(z)
Bonjour Lake, merci pour ta réponse.
Quelle est la règle générale pour résoudre ce genre d'exercices?
Merci pour vos réponses.
donc j'ai
P(z)= a(z-b)(z+1-3)(z+1+3)
Pourquoi a(z-b)? Je pensais que ça serait (az+b)(q(z)
tout polynome de degré n admet n racines dans C ...
donc connaissant deux racines d'un polynômes de degré trois c'est qu'il en manque une ...
tobi @ 05-11-2015 à 18:54
P(z)= a(z-b)(z+1-3)(z+1+3)
Pourquoi a(z-b)? Je pensais que ça serait (az+b)(q(z)
P(z)= a(z-b)(z+1-
3)(z+1+3)
Pourquoi a(z-b)? Je pensais que ça serait (az+b)(q(z)
et tu ne vois pas qui est q(z) ?
Tu devrais être sur toi et même pas venir demander si tu as bon : il te suffit de développer ...
Il faut pas être partisan du moindre effort intellectuel sinon tu n'avanceras jamais ...
D'autant plus que devant ton DS tu pourras pas demander : j'ai bon là ?
(z + 1 - i.V3).(z + 1 + i.V3) = (z+1)² + 3 = z² + 2z + 4
P(z) est donc factorisable par (z² + 2z + 4)
Division euclidienne :
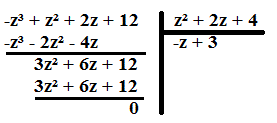
z = 3 est la 3ème racine.
Sauf distraction.
Crois mois Jygz quand j'ai posé la question je ne savais pas qu'il fallait développer, je m'en suis rendu compte juste après.
Merci de votre aide
Jygz @ 06-11-2015 à 02:29
Tu devrais être sur toi et même pas venir demander si tu as bon : il te suffit de développer ...
Il faut pas être partisan du moindre effort intellectuel sinon tu n'avanceras jamais ...
D'autant plus que devant ton DS tu pourras pas demander : j'ai bon là ?
Tu devrais être sur toi et même pas venir demander si tu as bon : il te suffit de développer ...
Il faut pas être partisan du moindre effort intellectuel sinon tu n'avanceras jamais ...
D'autant plus que devant ton DS tu pourras pas demander : j'ai bon là ?
bonsoir
et au delà de ça, dans la vie active, d'ici quoi ? trois, cinq ans ? tu ne pourras même pas attendre qu'un prof ait corrigé ton DS pour savoir si tu "avais bon" ... Quand ton patron te donnera un problème à résoudre, il ne l'aura pas fait juste avant pour pouvoir vérifier si ce que tu lui proposes comme solution est correct .... sinon, il n'aurait plus besoin de te demander de t'en occuper !
Il est donc temps de commencer à apprendre à vérifier toi-même tes calculs, méthodes, démarches, chaque fois que tu le peux.