Annuler
connectez vous
analyse complexe en post-bac
- Les nombres complexes - supérieur
- Nombres complexes : les classiques
- Ensemble et application Partie II
- Équations différentielles : un Cours complet avec des exemples
- Généralités sur les matrices, applications linéaires, changement de base, rang d'une matrice - supérieur
- Espaces vectoriels et Applications linéaires - supérieur
- Un best-of d'exos de probabilités (après le bac)
Inscription / Connexion Nouveau Sujet
Accueil l'île des mathématiques Forum de mathématiquesListe de tous les forums de mathématiques SupérieurOn parle exclusivement de maths, pour le supérieur principalement, les BTS, IUT, prépas... Licence Maths 1e ann Analyse complexeTopics traitant de analyse complexe [tout]Lister tous les topics de mathématiques
Niveau Licence Maths 1e ann
intégrales généralisés et théorèmes des résidus
Posté par lachgar
Bonjour à tous .
Est ce qu'il existe une méthode spécifique pour calculer un intégrale avec l'infini aux bornes ?
par exemple:
Merci beaucoup.
Bah oui comme tu dis théorème des résidus!
Tu prends comme chemin le demi cercle de rayon R dans la partie haute du plan complexe et tu fais tendre R vers l'infini
Ici on peut trouver une primitive et calculer l'intégrale.
on commence par décomposer en éléments simples
x²/((x²+3)x²+4)) = 4/(x²+4)-3/(x²+3) puis on intègre, ça donne des arctan, etc ...
Merci beaucoup pour vos réponses, mais la question était d'utiliser le théorème de résidus.
Donc est ce que j'obtiendrai le même résultat si je tend R vers l'infini ?
Bonjour lachgar
Eh bien, ce sera justement le moment de vérifier que tous les chemin mènent à Rome ! 
En principe OUI.
Tu dois intégrer la fonction tel que
, le long de l'axe réel entier dans le plan complexe.
Donc on prendra un demi cercle de rayon R de façon que les points singuliers du demi plan supérieur y soient à l'intérieur.
Nos points singuliers sont et
Donc les points à utiliser sont et
Razes @ 30-01-2017 à 15:51
En principe OUI.
Tu dois intégrer la fonction
tel que =\frac{z^2}{(z^2+3)(z^2+4)})
, le long de l'axe réel entier dans le plan complexe.
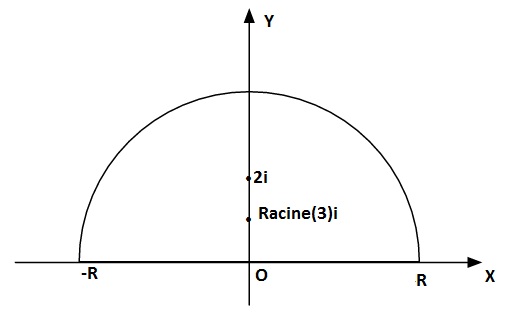
Donc on prendra un demi cercle de rayon R de façon que les points singuliers du demi plan supérieur y soient à l'intérieur.
Nos points singuliers sont
et 
Donc les points à utiliser sont
et 
En principe OUI.
Tu dois intégrer la fonction
Donc on prendra un demi cercle de rayon R de façon que les points singuliers du demi plan supérieur y soient à l'intérieur.
Nos points singuliers sont
Donc les points à utiliser sont
Puis on applique directement la relation :
N'est ce pas?
lionel52 @ 30-01-2017 à 16:11
Bah y a 2 points singuliers donc tu choisis quoi pour z0?
Je pense que je dois les choisir tous les deux ( 2i et Bah y a 2 points singuliers donc tu choisis quoi pour z0?
Puisqu'ils sont tous avec des parties imaginaires positives.
Merci beaucoup ,mais pourquoi on doit toujours préciser qu'il s'agit d'un demi cercle ,alors qu'on peut tout simplement dire les Res(f,z) tel que Im(z)
0 ?
C'est toujours sympa des demi-cercles. Mais tu peux évidemment prendre des chemins du diable quelconques autour des singularités et ... euh ! bah ! sans moi ...
rebonjour.
Je sais bien que le chemin pris est un demi cercle ,mais ce que je veux dire c'est que le demi cercle n'intervient pas dans les calcules selon les réponses ci-dessus . Donc on peut simplement conditionner aux singularités qu'elles aient une partie imaginaire positive
Tout à fait on peut prendre un chemin quelconque. Mais c'est plus judicieux d'utiliser des cercles et demis cercles quand souhaitent majorer la fonction.
Ton expression de l'intégrale est en partie fausse car tu as négligé un terme sans en apporter la preuve.
On doit démontrer que l'intégrale est egale à zéro et c'est là ou le choix du demi cercle devient intéressant.
Et le but c'est d'avoir un chemin qui reproduise l'intervalle ]-oo;+oo[. Avec un demi cercle, la base la reproduit. Avec un cercle pas vraiment !
Razes @ 30-01-2017 à 17:55
Tout à fait on peut prendre un chemin quelconque. Mais c'est plus judicieux d'utiliser des cercles et demis cercles quand souhaitent majorer la fonction.
Ton expression de l'intégrale est en partie fausse car tu as négligé un terme sans en apporter la preuve.
 dz+\int_{C }{f(z) dz=}2i\pi( Res(f,z_1)+Res(f,z_{z_2})))
On doit démontrer que l'intégrale dz)
est égale à zéro et c'est là ou le choix du demi cercle devient intéressant.
Tout à fait on peut prendre un chemin quelconque. Mais c'est plus judicieux d'utiliser des cercles et demis cercles quand souhaitent majorer la fonction.
Ton expression de l'intégrale est en partie fausse car tu as négligé un terme sans en apporter la preuve.
On doit démontrer que l'intégrale
Alors là je suis d'accord .
Dans le cours on montre par l'inégalité de Cauchy que l'intégral sur le premier chemin (
j'aurais la montré avec le théorème des résidus ,mais sur le dessin, les singularités sont à l'intérieure du demi cercle, donc ça ne sera pas 0.
L'intégrale sur le demi cercle + base est constante et vaut la somme des 2 résidus
L'intégrale sur [-R,R] tend vers l'intégrale que tu cherches
L'intégrale sur le demi cercle tend vers 0 quand R->+oo
Razes @ 30-01-2017 à 18:53
C'est sur que ça aider.
C'est sur que ça aider.
Parce que cette condition est donné au début de de la propriété dans mon cours, et je pense que nous travaillons qu'avec ce genre ,et c'est pour ce la qu'on a montré que le deuxième terme est nul.
N'est ce pas?
Razes @ 30-01-2017 à 19:58
Dommage pour le match d'hier.
C'est pas grave On est déjà en quart de finale...hahahaDommage pour le match d'hier.
Oui, c'est ça.
Pour le match, on aurait pu gagner. Mais on a gagné un bon entraineur et on s'est débarrassé de cette racaille de Zaki.