Contour

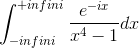
Bonjour marco15
Tu coupes ton cercle de centre 0 et de rayon a en 4 quarts de cercles . Et non pas en demis-cercles.

Comment dois-je séparer les quartes de cercle? Ils doivent former un Plus ou une croix?

Je ne vois pas en quoi prendre des quarts de cercle va arranger mon problème ... je cherche une intégrale de -inf à + inf, il faut donc que je prenne l'axe des abscisses

J'ai tenté de dessiner une croix de Saint André dans mon cercle, j'ai fait comme j'ai pu.
Tes singularités vont être isolées.
Tu travailles dans chacun des quarts de cercles.

Ok ! Un X permettant d'isoler chaque singularité...
Mais du coup je ne comprends pas la finalité, comment vais-je retomber sur l'intégrale de -inf à + inf puisque aucun contour ne prend l'axe des absisces ?

Oui, en effet, alors là, il faudrait que je fasse un dessin, sinon, ça va être chaud à expliquer !

Oui ^^
Pouvez-vous essayer de m'expliquer comment ce découpage permettrait de sortir l'intégrale de -inf à +inf?

Je vais essayer :
On va faire par 1/2 cercles.

1/ Demi-cercle Im(z) >= 0.
Tu choisis > 0, très petit.
Tu pars du point z = -2.
Sur ton segment [-2,2], tu ôtes
- la partie ]-1-, -1+[ et tu remplaces par le 1/2 cercle de centre -1 et de rayon et Im(z) >= 0,
- la partie ]1-, 1+[ et tu remplaces par le 1/2 cercle de centre 1 et de rayon et Im(z) >= 0.
A partir du point 2, tu traces un 1/4 de cercle de centre 0 et de rayon 2 vers le point 2i.
Tu redescends vers la troisième singularité, i, avec le même procédé, mais cette singularité, tu l'entoures du cercle de centre i et de rayon .
Tu remontes vers 2i puis tu redescends vers -2 en quart de cercle.

2/ 1/ Demi-cercle Im(z) <= 0.
Même .
Tu pars du point z = -2.
Sur ton segment [-2,2], tu ôtes
- la partie ]-1-, -1+[ et tu remplaces par le 1/2 cercle de centre -1 et de rayon et Im(z) >= 0,  Im(z) <= 0.
- la partie ]1-, 1+[ et tu remplaces par le 1/2 cercle de centre 1 et de rayon et Im(z) >= 0,  Im(z) <= 0.
A partir du point 2, tu traces un 1/4 de cercle de centre 0 et de rayon 2,  vers le point -2i.
Tu remontes vers la quatrième singularité, -i, avec le même procédé, mais cette singularité, tu l'entoures du cercle de centre -i et de rayon .
Tu redescends vers -2i puis tu remontes vers -2 en quart de cercle.

Espérant que ce soit lisible.

Bonjour,
c'est tout a fait lisible
j'ai un cercle avec 4 "trous"  .
j'ai le contour suivant (vérifions que nous parlons de la même chose avant d'aller plus loin!)

je pars de 2 je monte en quart de cercle de centre de centre 0 de rayon 2 jusqu'à 2i, depuis 2i je redescneds jusqu-à i que j'entoure d'un centre de centre i de rayon epsilon, ce tour effectué je remonte à 2i puis je descends jusqu'à -2i le long d'un demi cercle de centre 0 de rayon 2 (c'est là que je pense n'avoit peut-être pas compris) , depuis -2i je remonte jusqu'à -i, je l'entoure et je redscends jusqu'à -2i puis je remonte jusqu'à 2i le long d'un demi cercle de centre 0 et de rayon 2

Ceci fait, "j'entoure" -1 d'un cercle de centre epsilon idem pour 1

Sommes-nous d'accord?

En fait je doute entre deux contours :
celui que j'ai décrit où [-2,2] n'appartient pas au contour (ce segment est inclus dans le domaine, points -1 et 1 exclus)

ou un autre contour ou  [-2,2 ] (-1 et 1 exclus ) fait partie du contour, cette option m'a l'air étrange car dans ce cas j'aurai dessiné deux domaines symétriques par rapport à l'axes des réels

Désolé pour le triple post, mais au moins j'aurai posé toutes mes questions.
Pourquoi proposer de travailler sur le plan entier et pas seulement sur le plan supérieur (Im(z) >= 0) ?

On parle pas de la même chose.

Tu pars de 2 (si tu veux).
Tu montes en 1/4 cercle jusqu'à 2i.
Tu descends jusqu'à i + .i.
Tu contournes i du cercle de centre i et de rayon .
Tu remontes jusqu'à 2i.
Tu redescends en 1/4 cercle jusqu'à -2.
Tu vas jusqu'à -1-.
Tu passes par dessus -1 en un demi-cercle de rayon .
Tu files de -1+ jusqu'à 1-.
Tu passes par dessus 1 en un demi-cercle de rayon .
Tu files de 1+ à 2.
Le premier 1/2 cercle est bouclé.

Tu repars de 2 .
Tu descends en 1/4 cercle jusqu'à -2i.
Tu remontes jusqu'à -i - i.
Tu contournes -i du cercle de centre -i et de rayon .
Tu redescends jusqu'à -2i.
Tu remontes en 1/4 cercle jusqu'à -2.
Tu vas jusqu'à -1-.
Tu passes par dessous -1 en un demi-cercle de rayon .
Tu files de -1+ jusqu'à 1-.
Tu passes par dessous 1 en un demi-cercle de rayon .
Tu files de 1+ à 2.
Le second 1/2 cercle est bouclé.

Parfait,
j'avais fait ce type de contour au début, mais quel est l'intérêt d'en faire deux?
Et pourquoi ne garde-t-on pas i et -i pour appliquer le théorème des résidus?

Désolé de poser beaucoup de questions, mais j'aime bien comprendre où va me mener un choix^^

Mais oui bien sur !!!!!! Le demi cercle inférieur sur celui ci sin est négatif et je peux utiliser le second lemme de jordan pour faire disparaître l'intégrale le long du demi cercle de centre 0 et de rayon 2 car

|z|*|e^iz / (z^4+1)|= R*(e^(Rsin(theta)) )/ |z^4 + 1 | qui équivaut quand R tend vers l'infini à :

e^Rsin(theta) / R^3  or sur le demi cercle inférieur sin theta <= 0 donc il ya convergence de la borne supérieure vers 0 donc convergence absolue et le théoreme de Jordan est valable


!
J'essaie de rédiger mon exo et je vous envoie mon résultat sur ce forum, pourrez vous me confirmer ou non?
merci !

heu c'est z^4 - 1  et pas +1 ^^ mais cela ne change pas grand chose

On fait comme ça (là je dois y aller).

Tu dois avoir Res_-i f = Lim (z-i) (z+i)f(z) = (sauf erreur)

Et donc, l'intégrale le long du contour =

Où c'est   z^4 - 1    ?

Donc

C'est donc bon pour le résidu avec : il y avait faute de frappe, mais j'ai bien continué

Si f(x) = exp(ix)/(x⁴ - 1)  pour x réel distinct de 1 et -1 ,  f n'est pas intégrable sur ( ni  "d'intégrale convergente " )

Ok

je prend le demi plan inférieur, j'oriente dans le sens direct je prends B réel postif et A réel négatif tel que [0B] et[AO] soient de longueur R.
je pose z=Re^i*theta
Intégrale f(z) dz = 2*i*pi*res(f,-i)=pi/2*e
(théoreme des résidus : f est holomorphe sauf en -i qui est un pôle simple

mais
intégrale f(z)dz = intégrale sur le segment BA + intégrale le long de l'arc de cercle AB - intégrale le long de l'arc de cercle autour de 1 - l'intégrale le long de l'arc de cercle -1

quand on passe à la limite quand epsilon tend vers 0 et R tend vers l'infini

On a intégrale le long de l'arc de cercle AB qui tend vers 0 (second lemme de jordan (ca marche car on a pris le demi cercle inférieur donc le produit |z| |f(z)| tend vers 0 quand R tend vers l'infini (je ne fais pas le dévelopmment ) )

Intragrale sur le segment BA = - Intégrale sur le segment AB qui tend vers - intégrale désirée (celle dont on veut avoir la valeur)

intégrale le long de l'arc de cercle de centre -1 ; d'apres le troisieme lemme de jordan, quand epsilon tend vers 0 cette intégrale tend vers
i*(angle d'arrivée - angle de départ)*Res(f,-1) = i * (-pi - 0 )* res(f,-1)
                                                                                                    = - i  * pi * (-e^i / 4)

de même intégrale le long de l'arc de cercle de centre 1
= i*(-pi - 0) * res(f,1)=-i*pi*(e^(-i) / 4 )


AU FINAL

J= (i*pi/4 ) * (e^-i  - e^i) - pi/2e


visiblement je ne trouve pas comme vous...

Il me semble que vous avez oublié de retirer les demi cercles de centre -1 et 1 avec le troisieme lemme de jordan
Je pense aussi qu'il y a un problème de signe , si on parcourt dans le sens direct alors on calcule l'intégrale de +inf à -inf ! donc il faut prendre le signe opposé

Laisse tomber, n'existe pas !

C'est ce que j'ai mis dans mon post de 18:04 qu'il faut travailler.

C'est un exo de partiels de l'année dernière, je pense qu'il existe une solution ? Comments pouvez-vous dire à coup sur que cette intégrale n'existe pas?

Quel est l'équivalent de exp(ix)/(x⁴ - 1) quand x tend vers 1 ?

c'est exp(-ix)/(x^4 - 1 ) bah quand x tend vers 1 x^4 - 1 tend vers 0 donc f(x) tend vers l'infini ...effectivement.
Mais ça signifie juste que l'intégrale est généralisée en 1, ça ne signifie pas forcément qu'il n'y a pas convergence... si?

l'équivalent ????

Je suis perdu, équivalent en 1 ? Je n'ai fait que des équivalents en 0 et +inf !
Que voulez-vous me montrer?

en 1. Donc a même nature de convergence pour vers 0 que qui ne converge pas du tout.

En l'infini, ok. Pas en 1 (ou -1).

Je suis définitivement perdu
Vous êtes ne train de me dire que l'on ne peut pas calculer cette intégrale?

Pardon :

en 1. Donc a même nature de convergence pour vers 0 que qui ne converge pas du tout.

Pourtant mon raisonnement m'avait l'air cohérent ... ^^

En + , d'accord , faut toujours regarder
Mais pourquoi en 0 ?   f(0 n'existe pas ?

Plusieurs questions :
Peut -on calculer e^-ix / (x^4-1) entre - inf et +inf
Si oui, mon raisonnement est -il correct?
Si non, pourquoi mon raisonnement est - il incorrect, j'ai l'impression d'avoir bien respecté toutes les conditions de mes théorèmes

Pourquoi tu ne réponds pas à ce que je te demande ?

Je n'ai pas tout lu  ce que tu as fait mais il me semble que tu n'as pas regardé ce qu'il se passe autour de 1 et -1 , la où il y a problème .

Je ne comprends pas ce que vous voulez que je vous réponde autour de 1 et -1

f(x) equivaut à 1/(x^4-1) en 1 et -1

Heu pardon je dis n'importe quoi

en 1 e-ix = e-i
en -1 e-ix = e^i

Je vois pas ce que vous voulez que j'écrive

Quand x tend vers  de 1 , ex)(-ix)/(x⁴ - 1) est  équivalent à exp(-1)/4(x - 1) qui n'est pas intégrable sur ]1 , 2] ni sur [0 , 1[ .

Donc a fortiori pas intégrable sur [0, plus inf]...

Par contre, marco15, ce qui m'intéresserait, c'est d'avoir le sujet de partiel que tu évoquais le 28-10-16 à 18:47, histoire de voir le contexte.
Tu peux me l'envoyer par mail, s'il te plaît ? Je t'en remercie par avance.

Je ne me permettrais pas de divulguer un partiel de mon école (encore plus si il y  a des fautes!^^)
Cependant , pour le contexte c'est le suivant :

EXERCICE 2 : INTEGRATION DANS LE PLAN COMPLEXE

soit J= intégrale de e^-ix / x^4-1 dx

1) quelle fonction analytique est-il judicieux de choisis? Quelles sont ses singularités?
2) Choisissez un contour approprié
3) Calculer J

voila !

L'exercice 1 n'avait pas de lien avec le deuxieme

Bonjour,

Cf. également ceci .

Bonjour TP
La dernière réponse est particulièrement intéressante et correspond à ce que j'ai commencé à penser à un moment, savoir la présence d'une valeur principale devant l'intégrale pour en donner un sens.
C'est pour ça que j'ai dit à un moment " ... n'a aucune chance d'exister ?".
Mais sinon, en soi, le machin tel que présenté dans le post initial, n'a aucun sens.

Je ne comprends pas  tout, mais je trouve le même résultat que noix de toto à la fin

en remplaçant t par t=-1