- Les nombres complexes - supérieur
- Nombres complexes : les classiques
- Équations différentielles : un Cours complet avec des exemples
- Ensemble et application Partie II
- Espaces vectoriels et Applications linéaires - supérieur
- Généralités sur les matrices, applications linéaires, changement de base, rang d'une matrice - supérieur
- Ensemble et application Partie I
Inscription / Connexion Nouveau Sujet
le complexe
svp la solution du probleme et merci d'avance
"determiner l'ensemble des point complexe M(z) tel que (z-1)/(z-i)=2exp(i*(teta)) avec teta parcour toute l'ensemble R
Ca ne marche pas comme ça, ici. Le forum n'est pas un distributeur de corrigés pour étudiants qui ont la flemme.
Qu'as-tu essayé ?
Bonjour,
On suppose
Soit
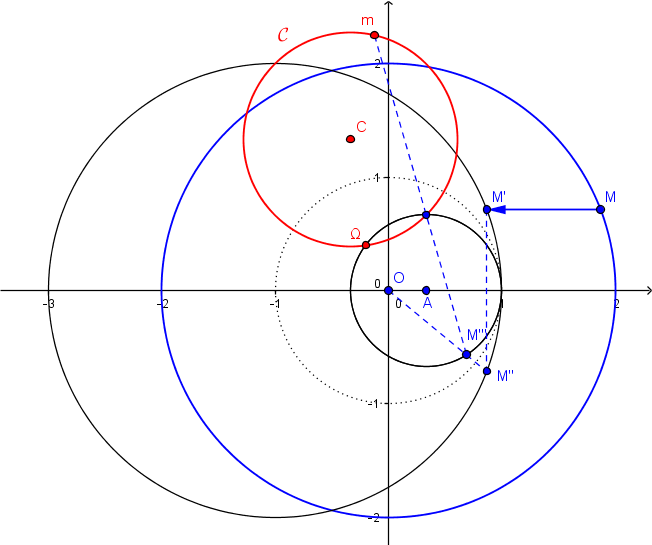
décrit le cercle de centre
et de rayon
quand
décrit
On cherche donc l' image d' un cercle par une homographie; on sait que c' est en général un cercle (ou éventuellement une droite).
Si on veut aller plus loin, on peut décomposer l' homographie en question:
Soit:
la translation:
la symétrie par rapport à l' axe des réels:
l' inversion de pôle
et de puissance
la similitude directe
On a
On trouve sans difficultés que l' image du cercle par
est le cercle de centre
et de rayon

Ben si, ça marche comme ça. Il y a des gens qui ont une vocation de distributeurs automatiques de corrigés pour les étudiants qui ont la flemme !



 analyse complexe en post-bac
analyse complexe en post-bac