Annuler
connectez vous
- Produit Scalaire dans l'espace - Cours terminale S
- Produit Scalaire dans l'espace - Exercice Terminale S
- Onze Exercices divers sur les vecteurs - première
- Fonction exponentielle - Fiche de Cours terminale
- Le raisonnement par récurrence : principe et exemples rédigés
- Limites de fonctions - Cours sur les limites
- Fiche sur les nombres complexes - terminale
- Cours sur les suites en Terminale S
Inscription / Connexion Nouveau Sujet
Accueil l'île des mathématiques Forum de mathématiquesListe de tous les forums de mathématiques LycéeOn parle exclusivement de maths, niveau lycée. TerminaleForum de terminale Produit scalaireTopics traitant de produit scalaire [tout]Lister tous les topics de mathématiques
Niveau terminale
Perpendiculaire commune...
Posté par Gwen03
Bonjour a tous la géométrie dans l'espace n'étant pas du tout mon fort je viens sollicité un peu d'aide ici en esperant que quelques personne pourront m'aidé a résoudre l'exercice suivant je vous en remercie d'avance 
!
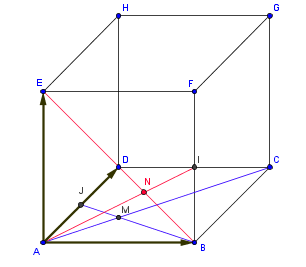
ABCDEFGH est un cube d'arete 1.
Les points I et J sont les milieux respectifs des cotés [BF] et [AD].
Les point M et N sont respectivement les points d'intersection des droites (BJ) et (AC) d'une part, (AI) et (BE) d'autre part
On se propose de démontrer de deux manieres que la droit (MN) est perpendiculaire commune aux diagonales (EB) et (AC).
1- Démontre que le point M est le centre de gravité du triangle BAD. De même quel est le centre de gravité du triangle ABF
2- UTILISATION DU REPERE ORTHONORME (A; AB; AD; AE) il y'a des vecteurs au desssus
a. Determiner les coordonnées du point M
b. Déterminer les coordonnées du point N
c. Calculer les produits scalaires MN.EB et MN.AC
3 UTILISATION CALCUL VECTORIEL
a. a l'aide de la relation de Chasle demontrer que :
MN=1/3DF
b.demontrer que DF.EB=0
c. Demontrer que DF.AC=0 et conclure
Bonjour Gwen03
1. Regarde la représentation de la face ABCD jointe ; le centre de gravité est l'intersection des médianes
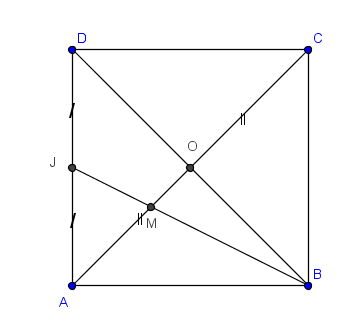
Cette première question te permet de donner les coordonnées de M , car le centre de gravité partage chaque médiane en 2 segments 2/3 et 1/3 , ( 2/3 à partir du sommet dont est issue cette médiane )
Ici , on a par exemple BM = 2/3 BJ
Non , M a pour coordonnées (1/3;1/3;0)
Regarde le schéma ; la 3ème coordonnées est nulle , car on se trouve dans le plan de base
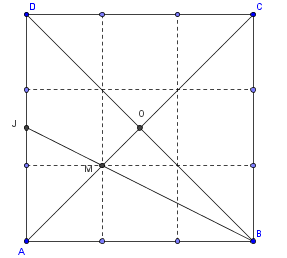
Ah oui merci et est-ce que le centre de gravité de ABF pour la question un sera le point N (0; 1/3; 1/3 ) ? Je suis vraiment nul :/
Comme on t'a demandé de déterminer les coordonnées de M et de N , calcule plutôt les coordonnées du vecteur MN , puis celles de EB
Petite aide : E(0;0;1) B(1;0;0)
Puis utilise la propriété 
(x;y;z).
(x';y';z')= xx' + yy' + zz'
Coordonnées de MN (xN-xM ; yN-yM ;zN-zM)
Donc MN (2/3-1/3 ; 0 - 1/3 ; 1/3-0) = ( ....
Refais aussi EB ; ce que tu as proposé est le vecteur nul , or très visiblement sur la figure , ce vecteur n'est pas nul 
On peut exprimer les 2 vecteurs MN et DF en fonction des vecteurs de base AB , AD et AE
Je te décompose MN :
MN = MA + AN = -1/3AB -1/3AD + 2/3 AB + 1/3AE = 1/3AB - 1/3AD + 1/3AE
Fais de même pour DF ( inspire toi de la figure sans oublier que BF est égal à AE )
Il faut que tu trouves une expression de DF en fonction de AB , AD et AE , pour pouvoir comparer avec MN , et conclure
Pourquoi ce signe "moins" devant DA ?
Et puis il reste toujours EF qui n'est pas un vecteur de base , mais qui est égal à ....???