- Description de mathématique formelle-termes et relations
- Théorèmes
- Théories logiques
- Ensemble et application Partie II
- Équations différentielles : un Cours complet avec des exemples
- Généralités sur les matrices, applications linéaires, changement de base, rang d'une matrice - supérieur
- Espaces vectoriels et Applications linéaires - supérieur
- Un best-of d'exos de probabilités (après le bac)
Inscription / Connexion Nouveau Sujet
Problème de géométrie combinatoire
Les cases d'un échiquier sont coloriées alternativement en rouge, bleu et vert de la façon suivante : chaque case rouge est suivie d'une case bleue ; chaque case bleue est suivie d'une case verte ; chaque case verte est suivie d'une case rouge. En notant
les nombres de cases rouges, bleues et vertes respectivement, montrer que :
Le premier point est assez facile à prouver. Par exemple, pour la première inégalité, on peut avoir une case bleue au centre et autour d'elle trois cases rouges et une case verte (voir pièce jointe). Donc potentiellement, il peut y avoir trois fois plus de cases rouges que de cases bleues.
Par contre, je ne vois pas comment prouver le second point ().

super !!!
ne comprends-tu pas que dans le plan ça ne veut rien dire !!!
peux-tu compléter ta figure pour montrer ce qui se passe sur un échiquier de 16 cases ?
parce que pour moi : (si) la case bleue suit la case rouge (de gauche) alors elle précède la case rouge de droite !!!
quant à la case rouge au dessus ... ben à part dire qu'elle est au-dessus ...
Bonjour,
cet "exemple" montre surtout que tu ne comprends pas la différence entre
"suivante" qui impose une notion d'ordre (la case "avant" et la cade "après")
et "adjacente" qui n'en contient pas
et qui ne peut pas être utilisée ici du tout, quoi que tu fasses
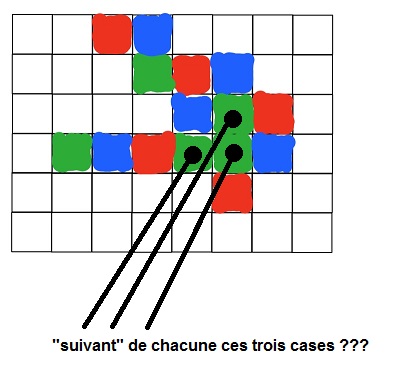
tes cases vertes adjacentes sont en violation totale avec
chaque case verte est "suivie" d'une case rouge.
vu que selon le sens (ordre !!) dans lequel on les parcours, il y a toujours une de ces cases vertes qui est "suivie" d'une case verte et pas rouge.
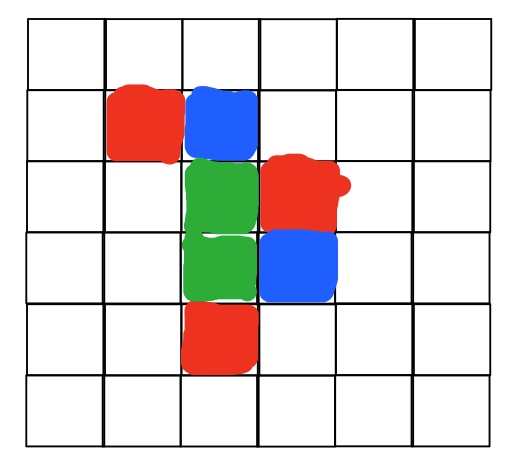
Effectivement le terme de "suivant" n'est pas adapté. En fait l'énoncé original1 parle de "cases à côtés" (donc ça correspond à "adjacent" il me semble). Donc en reformulant la partie de la consigne incriminée ça donne : "[...] chaque case rouge est à côté d'une case bleue ; chaque case bleue est à côté d'une case verte ; chaque case verte est à côté d'une case rouge [...]".
Du coup, il me semble que dans l'exemple ci-dessus, les trois cases vertes pointées par mathafou sont bien à côté d'une case rouge ; de même, les cases bleus sont à côté d'une case verte et les cases rouges sont à côté d'une case bleue.
1 : en pièce jointe un autre exemple donné avec l'énoncé original.
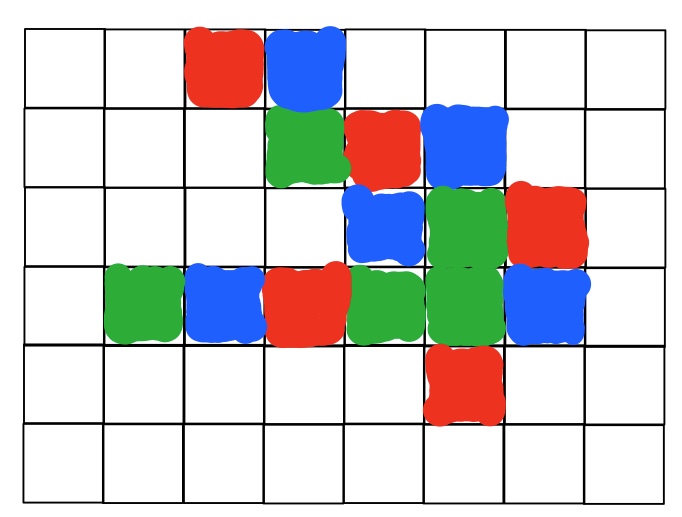
Et au départ on a quel choix ?
On choisit comment la couleur suivante ? Où ? Comment ?
Un énoncé mal résumé et mal raconté = aide inadaptée au problème posé 
De base l'énoncé est :
Les cases d'un échiquier de dimension
Mais on déduit facilement a) et b) des inégalités de la consigne que j'ai donnée ici.
Bonne nuit g0217d.
L'énoncé exact est plus court que celui que tu postas dans ton premier message.
Je me demande vraiment quel est l'intérêt que tu peux avoir à poster un énoncé erroné.
Merci pour vos remarques ; merci cocolaricotte et verdurin pour votre précieuse aide. Voici une solution (pour le deuxième point) qui je pense est correct. On construit itérativement une partition de l'échiquier en sous ensembles disjoints de la façon suivante :
on prend une case verte ;
ensuite, on lui associe toutes ses voisines1 bleues ;
enfin, on termine en ajoutant les voisines rouges des cases bleues de l'étape d'avant.
Cet algorithme génère quatre types de sous ensembles :
une case verte seule sans bleues ni rouges ;
une case verte avec une case bleue et de 0 à 3 rouges ;
une case verte avec deux bleues (deux configurations possibles) et de 0 à 6 rouges ;
une case verte avec trois bleues et de 0 à 7 rouges.
Cette partition est bien disjointe car les règles de coloriage décrites dans l'énoncé garantissent qu'une case bleue est forcément à côté d'une case verte donc elles "tombent" forcément dans un de ces sous ensembles ; de même, une case rouge est forcément à côté d'une case bleue donc elles "tombent" aussi dans un des sous ensembles de ses voisines bleues.
Dans chaque sous ensemble , on a
(
c'est la case verte de "départ") en notant
les nombres de cases rouge(s), bleue(s), verte du sous ensemble
. Donc en sommant sur tous les sous ensembles, on a bien
.
1 : c'est-à-dire des cases ayant un côté commun


 logique en post-bac
logique en post-bac