Inscription / Connexion Nouveau Sujet
Accueil l'île des mathématiques Forum de mathématiquesListe de tous les forums de mathématiques LycéeOn parle exclusivement de maths, niveau lycée. TerminaleForum de terminale Produit scalaireTopics traitant de produit scalaire [tout]Lister tous les topics de mathématiques

1 2 +

Niveau terminale
Partager :

Produit scalaire système d’équations

Posté par
sasul10001 13-02-22 à 14:11

Bonjour à vous,

J'ai un dm à faire, mais je suis bloqué sur l'exercice...
Voici l'énoncé : Dans un repère orthonormé, on considère le point F(1;0) et un point variable A(0;t) sur l'axe des ordonnés avec t

. On appelle strophoïde l'ensemble S'= S{F}.
Il existe deux réels x et y, on note P la propriété :

x^2+(y-t)^2 = t^2          
y = t(1-x)

avec t

1) démontrer que M(x;y) S si et seulement si P est vérifiée.

Ce que j'ai fait :

On calcule le vecteur AF :
J'ai trouvé comme coordonnées:
x du vecteur AF =1 ; y du vecteur AF = - t
Soit M(x;y) un point appartenant à la droite (AF) , vecteur AM =t vecteur AF

J'ai trouvé vecteur AF(1;-t) vecteur directeur de la droite (AF)

= t
.
.
.
J'ai trouvé :
x=t
y=t-t^2

on résous un système  : (J'en suis ici)
x= t
y=t-t^2

x=t
y=t(1-t)

x=t
y=t(1-x)

x=t
y+t^2=t

x=y+t^2
t=y+t^2

x-y=t^2
y=t-t^2

x-y=t^2
y=t(1-t)

x-y=t^2
y=t(1-x)


Après je ne sais pas comment je peut transformer la première équation en  x^2+(y-t)^2=t^2


Quelqu'un peut m'aider à résoudre le système s'il vous plaît ?

Merci

Posté par
sasul10001re : Produit scalaire système d’équations 13-02-22 à 14:13

*vecteur AM = tvecteur AF

Posté par
lakere : Produit scalaire système d’équations 13-02-22 à 14:25

Bonjour,

Ton énoncé est incomplet et tel quel incompréhensible.

Si tu veux des réponses adaptées, tu dois le recopier sans y changer ne serait-ce qu'une virgule.

Posté par
sasul10001re : Produit scalaire système d’équations 13-02-22 à 14:50

D'accord merci , c'est vrai que j'ai oublié des phases..


Dans un repère orthonormé, on considère le point F(1;0) et un point variable A(0;t) sur l'axe des ordonnés avec t . On appelle S l'ensemble des points M de la droite (AF) tels que MA=OA lorsque A varie sur l'axe des ordonnés et on appelle  strophoïde l'ensemble S'= S{F}.
Étant  donné deux réels x et y, on note P la propriété :

(Il s'agit d'un système à deux équations, je n'arrive pas à mettre l'accolade)
x^2+(y-t)^2 = t^2          
y = t(1-x)


Voilà j'espère que c'est clair

Posté par
sasul10001re : Produit scalaire système d’équations 13-02-22 à 14:53

sasul10001 @ 13-02-2022 à 14:50

D'accord merci , c'est vrai que j'ai oublié des phases..


Dans un repère orthonormé, on considère le point F(1;0) et un point variable A(0;t) sur l'axe des ordonnés avec t . On appelle S l'ensemble des points M de la droite (AF) tels que MA=OA lorsque A varie sur l'axe des ordonnés et on appelle  strophoïde l'ensemble S'=S{F}.
Étant  donné deux réels x et y, on note P la propriété :

(Il s'agit d'un système à deux équations, je n'arrive pas à mettre l'accolade)
x^2+(y-t)^2 = t^2          
y = t(1-x)


Voilà j'espère que c'est clair

Posté par
sasul10001re : Produit scalaire système d’équations 13-02-22 à 14:58

La première question est :
1) Démontrer que M(x;y) S si et seulement si P est vérifiée.

Posté par
lakere : Produit scalaire système d’équations 13-02-22 à 15:02

C'est beaucoup mieux.

Donc M(x,y)\in S\Longleftrightarrow\begin{cases}MA^2=OA^2\\\vec{FM}\text{  et  }\vec{AF}\text{  colinéaires }\end{cases}

Il y a deux conditions.

Essaie déjà d'écrire la première à l'aide des coordonnées de tes points.

Posté par
lakere : Produit scalaire système d’équations 13-02-22 à 15:29

Au fait, je viens de voir ceci (relatif à la seconde condition) :

  

Citation :
Soit M(x;y) un point appartenant à la droite (AF) , vecteur AM =t vecteur AF


tu as choisi pour notation t pour le réel.
Surtout pas : un réel k qui n'a rien à voir avec t déjà utilisé et que tu élimines entre deux équations.

Posté par
sasul10001re : Produit scalaire système d’équations 13-02-22 à 15:36

xAM =x -xA
yAM =y -yA



xAM= x-0 =x
yAM= y- t

et

xAO=x-0=x
yAO=x -t

AM=AO

Donc les droites (AM) et (AO) sont parallèles ?

Posté par
lakere : Produit scalaire système d’équations 13-02-22 à 15:45

Citation :
xAO=x-0=x
yAO=x -t


Non : A(0,t) et O(0,0)

\vec{OA}(0,t) donc AO^2=OA^2=t^2

Je te rappelle la formule générale : AB^2=(x_B-x_A)^2+(y_B-y_A)^2

Il faut calculer de la même manière AM^2=MA^2 et écrire que les deux quantités sont égales soit MA^2=OA^2

Posté par
sasul10001re : Produit scalaire système d’équations 13-02-22 à 15:45

Pour la deuxième condition j'ai trouvé :

FM = tAF
xM -xF =t xAF
yM -yF = tYAF

x= xF+ t xAF
y=yF + t yAF

x=1+t
y=-t^2

Posté par
lakere : Produit scalaire système d’équations 13-02-22 à 15:47

D'abord la première condition. On viendra à la seconde ensuite (je t'ai fait une remarque à son sujet au dessus).

Posté par
sasul10001re : Produit scalaire système d’équations 13-02-22 à 16:00

D'accord

On a trouvé:
-  A(0;t) et O(0;0)
- OA (0;t) donc AO^2=OA^2=t^2
- AO^2=(xO-xA)^2 + (yO-yA)^2= (0-0)^2 + (0- t)^2 =t^2

j'ai trouvé

- A(0;t) et M(x;y)
- AM (x; y-t)
AM^2 = (y-t)^2

C'est juste ?

Posté par
lakere : Produit scalaire système d’équations 13-02-22 à 16:04

Citation :
AM^2 = (y-t)^2


Je crois qu'il manque un x^2 dans le second membre.

Et ensuite tu écris que AM^2=OA^2 \\

Posté par
sasul10001re : Produit scalaire système d’équations 13-02-22 à 16:04

Donc AM^2 = OA^2
             (y-t)^2= t^2

Posté par
lakere : Produit scalaire système d’équations 13-02-22 à 16:05

Citation :
Citation :
AM^2 = (y-t)^2


Je crois qu'il manque un x^2 dans le second membre.

Posté par
sasul10001re : Produit scalaire système d’équations 13-02-22 à 16:08

Ah ouii merci

AM^2= (x-0)^2 + (y-t) ^2 = x^2 +(y-t)^2

Posté par
sasul10001re : Produit scalaire système d’équations 13-02-22 à 16:09

sasul10001 @ 13-02-2022 à 16:04

Donc AM^2 = OA^2
             x^2+(y-t)^2= t^2

Posté par
lakere : Produit scalaire système d’équations 13-02-22 à 16:15

Bien, tu tiens la première équation de ta propriété P.

Passons à la seconde condition :

  

  

Citation :
Citation :
Soit M(x;y) un point appartenant à la droite (AF) , vecteur AM =t vecteur AF


tu as choisi pour notation t pour le réel.
Surtout pas : un réel k qui n'a rien à voir avec t déjà utilisé et que tu élimines entre deux équations.


Reprends tes calculs avec un coefficient k et surtout pas t.

Tu vas obtenir un système de deux équations qui  dépendent de x,y,k et t

On "éliminera" ensuite k entre ces deux équations.
Mais d'abord, le système.

  

Posté par
sasul10001re : Produit scalaire système d’équations 13-02-22 à 16:34

sasul10001 @ 13-02-2022 à 15:45

Pour la deuxième condition j'ai trouvé :

FM = kAF
xM -xF =k xAF
yM -yF = kYAF

x= xF+ k xAF
y=yF + k yAF

x=1+k
y=-kt


J'ai  trouvé  ceci

Posté par
lakere : Produit scalaire système d’équations 13-02-22 à 16:37

Oui. Il reste à "éliminer" k entre ces deux dernières équations :

de la première, tu tires k=x-1 et tu remplaces dans la seconde.

Ça donne quoi ?

Posté par
sasul10001re : Produit scalaire système d’équations 13-02-22 à 16:39

sasul10001 @ 13-02-2022 à 16:34

sasul10001 @ 13-02-2022 à 15:45

Pour la deuxième condition j'ai trouvé :

FM = kAF
xM -xF =k xAF
yM -yF = kYAF

x= xF+ k xAF
y=yF + k yAF

x=1+k
y=-kt


k=x-1
y=-(x-1)t

k=x-1
y=t(1-x)

Donc il existe un réel t tel que

x^2+ (y-t)^2= t^2
y=t(x-1)


J'ai  trouvé  ceci

Posté par
lakere : Produit scalaire système d’équations 13-02-22 à 16:42

plutôt y=t(1-x) (tu as fait une erreur de signe).

Bon, voilà, tu tiens les deux équations de la propriété P.

Posté par
sasul10001re : Produit scalaire système d’équations 13-02-22 à 16:47

Ah oui j'ai mal tapé l'équation... wow merci de m'avoir aidé jusqu'au bout !! Vous êtes trèèès gentil ! bravo

Posté par
lakere : Produit scalaire système d’équations 13-02-22 à 16:50

Pour in formation, voici ta strophoïde et de rien sasul10001

Produit scalaire système d’équations

Posté par
sasul10001Produit scalaire système d’équations 13-02-22 à 18:16

Bonjour à tous,

J'ai un Dm à faire mais je n'avance pas trop.. voici l'énoncé :

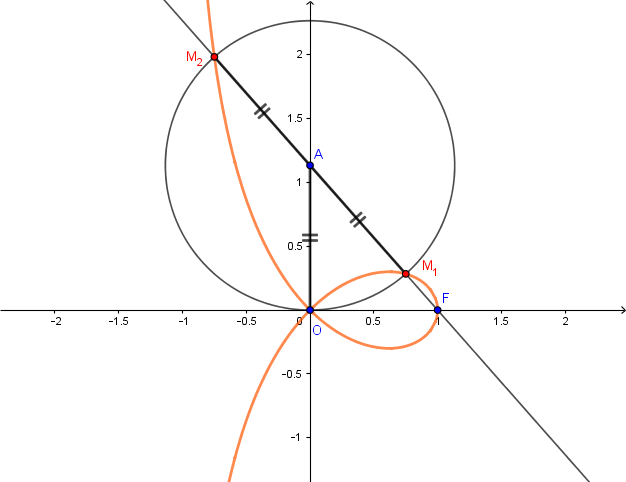
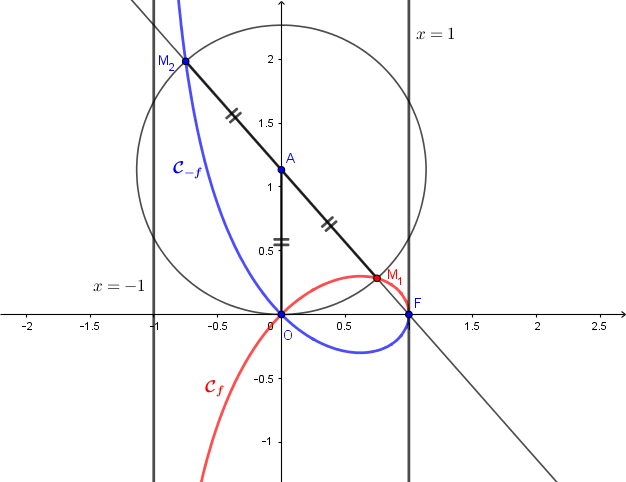
Dans un repère orthonormé, on considère le point F(1;0) et un point variable A(0;t) sur l'axe des ordonnés avec t   . On appelle S l'ensemble des points M de la droite (AF) tels que MA=OA lorsque A varie sur l'axe des ordonnés et on appelle  strophoïde l'ensemble S'=S{F}.
Étant  donné deux réels x et y, on note P la propriété :

(Il s'agit d'un système à deux équations, je n'arrive pas à mettre l'accolade)
x^2+(y-t)^2 = t^2          
y = t(1-x)

J'ai répondu à la première question qui était : 1) Démontrer que M(x;y) S si et seulement si P est vérifiée.

Il me reste les questions que je ne comprends pas)
2)a) Démontrer que si x alors on a l'équivalence :
P x^2(x-1)=y^2(1+x)

2)b) En déduire qu'un point M(x;y) appartient à la strophoïde si et seulement si x^2(x-1) = y^2(1+x)

3) Démontrer que si M(x;y) S' alors -1 <x1 . Comment se traduit-il graphiquement pour S' ?

4) Soit f la fonction définie sur ]-1;1] par f(x) =x (1-x/1+x). Démontrer que :
M(x;y) S' (y=f(x) ou y= -f(x))

En déduire que S' est la réunion des courbes de f et de -f.


Merci pour ceux qui m'aideront

*** message déplacé ***

Posté par
sasul10001re : Produit scalaire système d’équations 13-02-22 à 18:17

sasul10001 @ 13-02-2022 à 18:16

Bonjour à tous,

J'ai un Dm à faire mais je n'avance pas trop.. voici l'énoncé :

Dans un repère orthonormé, on considère le point F(1;0) et un point variable A(0;t) sur l'axe des ordonnés avec t   . On appelle S l'ensemble des points M de la droite (AF) tels que MA=OA lorsque A varie sur l'axe des ordonnés et on appelle  strophoïde l'ensemble S'=S{F}.
Étant  donné deux réels x et y, on note P la propriété :

(Il s'agit d'un système à deux équations, je n'arrive pas à mettre l'accolade)
x^2+(y-t)^2 = t^2          
y = t(1-x)

J'ai répondu à la première question qui était : 1) Démontrer que M(x;y) S si et seulement si P est vérifiée.

Il me reste les questions : (que je ne comprends pas)
2)a) Démontrer que si x -1 alors on a l'équivalence :
P x^2(x-1)=y^2(1+x)

2)b) En déduire qu'un point M(x;y) appartient à la strophoïde si et seulement si x^2(x-1) = y^2(1+x)

3) Démontrer que si M(x;y) S' alors -1 <x1 . Comment se traduit-il graphiquement pour S' ?

4) Soit f la fonction définie sur ]-1;1] par f(x) =x (1-x/1+x). Démontrer que :
M(x;y) S' (y=f(x) ou y= -f(x))

En déduire que S' est la réunion des courbes de f et de -f.


Merci pour ceux qui m'aideront


*** message déplacé ***

Posté par
lakere : Produit scalaire système d’équations 13-02-22 à 18:33

Bonjour,

Tu aurais du poster ces questions à la suite de celles de l'autre sujet sur la strophoïde.
Je vais faire en sorte qu'ils soient réunis.

*** message déplacé ***

Posté par
sasul10001re : Produit scalaire système d’équations 13-02-22 à 18:46

Bonjour , oui je ne voulais pas vous déranger une nouvelle fois.. merci pour ce que vous faites

*** message déplacé ***

Posté par
lakere : Produit scalaire système d’équations 13-02-22 à 18:48

J'attends que les deux sujets soient réunis par un modérateur pour poursuivre ...

*** message déplacé ***

Posté par
malou Webmasterre : Produit scalaire système d’équations 13-02-22 à 19:01

Bonsoir
c'est réuni !
bon courage pour la suite

Posté par
lakere : Produit scalaire système d’équations 13-02-22 à 19:07

2)a) De la seconde équation de P, tu tires, avec x\not=1 :

t=\dfrac{y}{1-x}

et tu remplaces t dans la première. Il faut procéder à quelques calculs (développements, regroupements...) mais tu dois arriver à l'équation demandée.

Posté par
lakere : Produit scalaire système d’équations 13-02-22 à 19:07

Et merci malou !

Posté par
lakere : Produit scalaire système d’équations 13-02-22 à 19:26

>>sasul10001,

Je pense que tu as une erreur dans ton énoncé ici :
  

Citation :
P x^2(x-1)=y^2(1+x)


Plutôt P\Longleftrightarrow x^2({\red 1-x})=y^2(1+x)

erreur d'ailleurs reproduite dans 2)b).

Posté par
sasul10001re : Produit scalaire système d’équations 13-02-22 à 20:27

D'accord

Ma réponse a été effacée, je raccourci ce que j'ai trouvé :

x^2+(y-t)^2 =t^2
t=y/(1-x)

.....................

x^2(1-x)-y^2 x -y^2 =0
t=y/(1-x)


x^2(1-x)-y^2 x =y^2
t= y/(1-x)


x^2(1-x)= y^2 + y^2 x
t= y/(1-x)


x^2(1-x)= y^2(1+x)
t= y/(1-x)


Voilà

Posté par
lakere : Produit scalaire système d’équations 13-02-22 à 21:00

Oui. En toute logique, tu as prouvé que :

  P\Longrightarrow x^2(1-x)=y^2(1+x)

Il faudrait faire une réciproque qui consisterait à écrire que pour x\not=1, on pose t=\dfrac{y}{1-x} et "remonter" les calculs que tu viens de faire pour obtenir x^2+(y-t)^2=t^2

2)b) (en corrigeant l'erreur est immédiate.

J'espère que tu as réfléchi à 3)


  

Posté par
lakere : Produit scalaire système d’équations 13-02-22 à 21:17

Il y a tout de même un minuscule problème en 2)b) :

  

Citation :
2)b) En déduire qu'un point M(x;y) appartient à la strophoïde si et seulement si x^2(1-x) = y^2(1+x)


La strophoïde, c'est S'=S\cup\{F\}

Il faut vérifier que les coordonnées de F(1,0) vérifient l'équation x^2(1-x)=y^2(1+x)
Ce qui est vrai donc tout va bien.

Posté par
sasul10001re : Produit scalaire système d?équations 13-02-22 à 21:33

* Modération > Citation inutile effacée. *

D'accord
Si j'ai bien compris : on vérifie si les coordonnées  de F(1;0) vérifient l'équation x^2(1-x)=y^2(1+x)

xF^2(1-xF) = 0
et yF^2(1+yF) =0

Donc x^2(1-x)=y^2(1+x)  donc M(x;y) appartient à S'= S {F}

Posté par
sasul10001re : Produit scalaire système d’équations 13-02-22 à 21:47

Pour la 3) j'ai trouvé :

Soit M(x;y) S' si est seulement si  -1<x 1
                              -1<xF 1
                              -1< 1 1
Donc la propriété P est vraie

‘Comment se traduit-il graphiquement pour S' ?'

La strophoïde passe par le point M (x;y) ?

Posté par
lakere : Produit scalaire système d’équations 13-02-22 à 21:47

Plus exactement F(1,0) appartient bien à la courbe d'équation x^2(1-x)=y^2(1+x)

  et c'est seulement maintenant qu'on peut écrire :

   M(x,y)\in S'\Longleftrightarrow x^2(1-x)=y^2(1+x)

Posté par
lakere : Produit scalaire système d’équations 13-02-22 à 22:00

3) Oh que non.

Ce n'est pas une équivalence qu'on te demande :

Citation :
3) Démontrer que si M(x;y) S' alors -1 <x1 .


C'est une implication.

  L'équation de S' : x^2(1-x)=y^2(1+x)

1) x=-1 dans cette équation donne 2=0

     donc x\not=-1

2) x^2(1-x)=y^2(1+x)

     on en déduit (si x et y  sont différents de 0) que 1-x et 1+x sont de même signe.

    donc que (1-x)(1+x)\geq 0 soit 1-x^2\geq 0 \\

   soit encore x^2\leq 1  d'où :

     -1\leq x\leq 1

Mais comme x\not=-1 (voir 1)), on a finalement ;

   -1<x\leq  1
  

Posté par
sasul10001re : Produit scalaire système d’équations 13-02-22 à 22:14

D'accord c'est plus clair

Posté par
lakere : Produit scalaire système d’équations 13-02-22 à 22:17

Quant à la question "graphique", je dirais que la courbe S' se trouve dans la bande verticale limitée par les deux droites verticales elles aussi d'équations x=-1 (exclue) et x=1 inclue.

La question 4) est relativement facile ...

Posté par
sasul10001re : Produit scalaire système d’équations 13-02-22 à 22:33

Pour 4) j'ai trouvé M(x;y) S' x^2(1-x)=y^2(1+x)
x^2 (1-x)/(1+x) =y^2

x^2 (1-x)/(1+x) = y

x(1-x)/(1+x) =y

Posté par
lakere : Produit scalaire système d’équations 13-02-22 à 22:43

4) Petite nuances :

  x\in]-1,1]

  x^2(1-x)=y^2(1+x)\Longleftrightarrow y^2=x^2\,\dfrac{1-x}{1+x}

et vu l'intervalle de définition pour x , on a \dfrac{1-x}{1+x}\geq 0

  et y^2=x^2\,\dfrac{1-x}{1+x}\Longleftrightarrow y=\pm x\,\sqrt{\dfrac{1-x}{1+x}}

Le signe  + correspond à f et le signe - à -f

Tu as mérité :

  1) Un nouveau dessin :

   Produit scalaire système d’équations

   2) Un lien pour tout savoir sur la strophoïde droite :  

Posté par
sasul10001re : Produit scalaire système d?équations 13-02-22 à 22:47

Olala merci c'est super intéressant !!

* Modération > Citation inutile effacée. *

Posté par
lakere : Produit scalaire système d’équations 13-02-22 à 22:49

De rien sasul10001 et bonne nuit

Posté par
sasul10001re : Produit scalaire système d’équations 14-02-22 à 09:17

Bonjour,
J'ai deux autres questions dans mon dm :
5) Démontrer que f'(x) = ( -x^2 - x+1)/(1+x)((1-x^2) . En déduire le tableau de variations de f et le compléter avec la limite de f en -1.

6) Construire S' dans un repère orthonormé du plan.

Est-ce que vous pouvez m'aider pour la 5) j'ai  trouvé :

Soit f définie par f(x) = x(1-x)/(1+x)
On dérive la fonction f avec u(x) = x ; u'(x)=1 ;     v(x)= (1-x)/(1+x) ; v'(x) = 1/2(1-x)/(1+x)  

J'ai trouvé :
f'(x)= u'(x)v(x) + u(x) v'(x)

        = (1-x)/(1+x) + x 1/2(1-x)/(1+x)

Ensuite je n'ai pas compris... est ce que je dois résoudre l'équation avec une fonction composée ?

Merci

Posté par
sasul10001re : Produit scalaire système d’équations 14-02-22 à 10:33

sasul10001 @ 14-02-2022 à 09:17



Est-ce que vous pouvez m'aider pour la 5) j'ai  trouvé :

Soit f définie par f(x) = x(1-x)/(1+x)
On dérive la fonction f avec u(x) = x ; u'(x)=1 ;     v(x)= (1-x)/(1+x) ; v'(x) = 1/2(1-x)/(1+x)  

Mais (1-x)/(1+x) = u(x)/v(x)  

Ce qui veut dire que : 1-x =u(x) ; -1=u'(x) ; 1+x = v(x) ; 1= v'(x)

Donc si je reprend mes calculs :

f'(x) = 1 (1-x)/(1+x) + x 1/2(1-x)/(1+x) u(x)/v(x)

         .......
        = (1-x)/(1+x) + x 1/2(1-x)/(1+x) -(1(1+x) -1(1-x))/ (1+x)^2  

        J'ai simplifié l'équation , réduit les termes au même dénominateur......

........  

       = ((1-x)/1+x)) + x (1+x)/ (1-x) (1+x)^2

..........

J'ai factoriser par 1+x :

f'(x) = ((1-x)(1+x)^2 - x(1+x)) / (1+x)(1-x) (1+x)^2

           = ((1+x)((1-x)(1+x) -x))/ (1- x^2) (1+x)^2

.......... j'ai simplifié, ce qui m'a donné :

          = (1^2 -x^2 -x)/(1-x^2) (1-x)

   f'(x)  = (-x^2 -x +1) / 1-x^2 (1+x)




Posté par
lakere : Produit scalaire système d’équations 14-02-22 à 11:22

Bonjour,

J'ai un peu de mal à te lire mais j'ai repéré ceci au début:

  

Citation :
On dérive la fonction f avec u(x) = x ; u'(x)=1 ;     v(x)= (1-x)/(1+x) ; v'(x) = 1/2(1-x)/(1+x)


  Non : v(x)=\sqrt{w(x)} avec w(x)=\dfrac{1-x}{1+x} d'où :

    v'(x)=\dfrac{w'(x)}{2\sqrt{w(x)}}

Pour contrôle, tu dois tomber sur :

    f'(x)=\dfrac{-x^2-x+1}{(1+x)^2\sqrt{\dfrac{1-x}{1+x}}}

Inutile de recopier tes calculs que j'ai de toute manière beaucoup de mal à lire. Si tu tombes sur ce résultat, c'est que c'est bon ...


  

1 2 +


Rechercher
Menu
Espace membre
Changer d'île

Vous devez être membre accéder à ce service...

Pas encore inscrit ?

1 compte par personne, multi-compte interdit !

Ou identifiez-vous :

Rester sur la page

Inscription gratuite

Fiches en rapport

parmi 1675 fiches de maths

Désolé, votre version d'Internet Explorer est plus que périmée ! Merci de le mettre à jour ou de télécharger Firefox ou Google Chrome pour utiliser le site. Votre ordinateur vous remerciera !