Inscription / Connexion Nouveau Sujet
Accueil l'île des mathématiques Forum de mathématiquesListe de tous les forums de mathématiques SupérieurOn parle exclusivement de maths, pour le supérieur principalement, les BTS, IUT, prépas... Licence Maths 1e ann AnalyseTopics traitant de analyse [tout]Lister tous les topics de mathématiques
Niveau Licence Maths 1e ann
Partager :

Riemann

Posté par
maths19 15-03-18 à 21:50

Bonjour

Soit f: [a,b ]=> une fonction de classe C2 . pour n * , on pose :

Sn= \frac{b-a}{n} \sum_{K=0}^{n-1} f(\frac{sk+sk+1}{2})  , ou sk= a =k \frac{b-a}{n}

1) Justifier que Sn   \int_a^{b} f(t) dt quand n   (REUSSI)

2) On pose M = sup {|f''(s)|};  s [a,b]

a) Montrer que pour tout m [a,b], on peut trouver une fonction afine \alpha telle que

\alpha(x) = f(m) et t [a,b] = |f(t)- \alpha(t)| ≤ M \frac{(t-m)^2}{2}

b) Soient u,v [a,b] avec u<v et soit  m=\frac{u+v}{2} . Montrer que pour toute fonction affine \alpha on a

\int_u^{v} \alpha(t) dt = (v-u) \alpha (m)
(REUSSI)

c) Déduire de (a) (b) que pour tout u<v dans [a,b] , on a :
\int_u^{v} f(t) dt - (v-u) f(\frac{u+v}{2}) ≤ M \frac{(b-a)^3}{24}
(REUSSI)

3) montrer que pour tout n * , on a

|Sn - \int_a^{b} f(t) dt| ≤ M \frac{(b-a)^3}{24n^2}

Pouvais vous m'aider pour la question 3

Pour la question 2)a je l'ai commencer partiellement pouvais vous m'aider a la finir egallement

MERCI

Posté par
maths19re : Riemann 15-03-18 à 21:53

Pour la 2) a j'ai fait
je me suis servi de la formule et de l'inégalité de taylor en disant


|f(b) - f(a) - (b-a)f'(a)| ≤ M \frac{((b-m)^2}{2}
Du coup b=t ici

|f(t) - f(a) - (t-a)f'(a)| ≤ M \frac{((t-m)^2}{2}

mais je ne sais pas comment faire apres pour retrouvrer le alpha

Posté par
jsvdbre : Riemann 16-03-18 à 01:16

Bonsoir maths19.
Je conserve ton topic.
Je réécris néanmoins quelques données de façon claire :

S_n= (b-a)\frac{1}{n} \sum_{k=0}^{n-1} f\left(\dfrac{s_k+s_{k+1}}{2}\right) \text{, où }s_k= a +\frac{k}{n}(b-a)

Posté par
maths19re : Riemann 16-03-18 à 02:41

non sk = a et sk = k \frac{b-a}{n}

Posté par
jsvdbre : Riemann 16-03-18 à 09:03

Ah non ! C'est ou l'un ou l'autre mais pas les deux.

Posté par
jsvdbre : Riemann 16-03-18 à 10:21

Juste une remarque sur la question 1)
Elle se traite de façon générale et c'est toujours le même argument : l'uniforme continuité de f sur [a;b].
Soit \varepsilon > 0.
Si à tout entier n assez grand, on associe une subdivision régulière de [a;b],\{a,x_1,\cdots,x_{n-1},b\}, alors le pas de la subdivision est suffisamment petit pour que sur chaque intervalle [x_k;x_{k+1}] f puisse être approximée par n'importe quelle de ses valeurs (disons f(x_{n,k}), x_{n,k}\in [x_k;x_{k+1}]), de sorte que l'erreur commise,sur cet intervalle, avec son intégrale soit au plus de \varepsilon/n.

Donc \left| \sum_{k=1}^{n}{\frac{f(x_{n,k})}{n}} - \int f \right| \leq \varepsilon

En particulier, en prenant x_{n,k} = \frac{s_k+s_{k+1}}{2} où s_k = a + \frac{k}{n}(b-a)

Posté par
maths19re : Riemann 16-03-18 à 10:33

Pourtant sur mon enoncé c'est écrit comme ca Mais la question 1 je l'ai déja fait J'ai besoin d'aide pour la 2a et la 3

Posté par
jsvdbre : Riemann 16-03-18 à 13:41

Le 2)a) n'est autre que la démonstration de la formule de Taylor à l'ordre 2.
Si tu veux, voici le raisonnement à faire :

Si g est une fonction C^2 sur un intervalle [a;b], on cherche un réel A tel qui vérifie g(b) = g(a) + (b-a)g'(a) + \frac{(b-a)^2}{2}A.

On pose alors la fonction \phi(x) = g(b) - g(x) -(b-x)g'(x) -\frac{(b-x)^2}{2}A.

Clairement : \phi est continue sur [a;b], dérivable sur [a;b] donc sur ]a;b[ et \phi(a) = \phi(b) = 0 : elle vérifie les hypothèses du théorème de Rolle.

Donc il existe un certain c \in ]a;b[ tel que \phi'(c) = 0. On dérive \phi et on trouve A = g''(c).

On applique alors ce résultat à la fonction f de l'énoncé avec t et m deux points quelconques de [a;b] et on trouve que :

il existe \xi \in [\min \{t,m\};\max \{t,m\}] \text{ tel que } \blue f(t) -f(m)-(t-m)f'(m) = \frac{(t-m)^2}{2}f''(c)

On pose \alpha (t) = (t-m)f'(m) + f(m) et on a pour tout m \in [a;b]

- \blue \alpha(m) = f(m)

- \blue \forall t \in [a;b],~|f(t) - \alpha(t)| \leq \frac{(t-m)^2}{2}M.

Posté par
jsvdbre : Riemann 16-03-18 à 14:22

Avant de traiter la 3), je pense qu'il faut reprendre l'énoncé :

Citation :
c) Déduire de (a) (b) que pour tout u<v dans [a,b] , on a : \int_u^{v} f(t) dt - (v-u) f(\frac{u+v}{2}) \leq M \frac{(b-a)^3}{24}

Ce serait clairement stupide comme majoration.
J'imagine que ça doit plutôt être \left|\int_u^{v} f(t) dt - (v-u) f(\frac{u+v}{2})\right| \leq M \frac{(v-u)^3}{24}

On pose m_k = \dfrac{s_k + s_{k+1}}{2}

On prend alors u = s_k = a + \frac{k}{n}(b-a) et v = s_{k+1} = a + \frac{k+1}{n}(b-a), et ce, nonobstant ce que la transcription de l'énoncé (sinon l'énoncé lui-même) veut bien nous faire croire.

Il vient alors en appliquant le c) rectifié :

\left|\int_{s_k}^{s_{k+1}}{f(\xi)d\xi} - (s_{k+1}-s_k)f\left(m_k\right)\right|\leq M\frac{(s_{k+1}-s_k)^3}{24}

Or s_{k+1}-s_k = \frac{b-a}{n} donc :

\left|\int_{s_k}^{s_{k+1}}{f(\xi)d\xi} - (\frac{b-a}{n})f\left(m_k\right)\right|\leq M\frac{(b-a)^3}{24n^3}

On note de plus que \sum_{k=0}^{n-1}{\int_{s_k}^{s_{k+1}}{f(\xi)d\xi}}=\int_{a}^{b}{f(\xi)d\xi}. On a alors :

\begin {aligned}{\blue \left |\int_{a}^{b}{f(\xi)d\xi}-S_n\right|} &= \left|\sum_{k=0}^{n-1}{\int_{s_k}^{s_{k+1}}{f(\xi)d\xi}} - \frac{b-a}{n}\sum_{k=0}^{n-1}f\left(m_k\right)\right| \\ & \leq \sum_{k=0}^{n-1}\left|\int_{s_k}^{s_{k+1}}{f(\xi)d\xi}-\frac{b-a}{n}f\left(m_k\right)\right| \\ & \leq Mn\frac{(b-a)^3}{24n^3}\\ &\blue \leq M\frac{(b-a)^3}{24n^2}\end{aligned}

Posté par
maths19re : Riemann 16-03-18 à 17:14

jsvdb @ 16-03-2018 à 14:22


\begin {aligned}{\blue \left |\int_{a}^{b}{f(\xi)d\xi}-S_n\right|} &= \left|\sum_{k=0}^{n-1}{\int_{s_k}^{s_{k+1}}{f(\xi)d\xi}} - \frac{b-a}{n}\sum_{k=0}^{n-1}f\left(m_k\right)\right| \\ & \leq \sum_{k=0}^{n-1}\left|\int_{s_k}^{s_{k+1}}{f(\xi)d\xi}-\frac{b-a}{n}f\left(m_k\right)\right| \\ & \leq Mn\frac{(b-a)^3}{24n^3}\\ &\blue \leq M\frac{(b-a)^3}{24n^2}\end{aligned}


je ne comprend pas pourquoi il y a Mn ??à l'avant derniere ligne

Posté par
maths19re : Riemann 16-03-18 à 18:07

J'ai oublier une question , avec ce qu'on à fait on doit trouver une valeur approchée de ln(3) à 10^-2 pres . pour faire ca on pose f(x) = 1/t  et on prend a = 1 et b= 3 mais apres je bloque avec la formule qu'on nous donne

Posté par
jsvdbre : Riemann 16-03-18 à 22:24

Citation :
je ne comprend pas pourquoi il y a Mn à l'avant derniere ligne

Parcequ'on somme n termes ayant même majorant.

Citation :
on doit trouver une valeur approchée de \ln(3) à 10^{-2} pres

On a \ln(3) = \int_{1}^{3}\frac{dt}{t}. Soit donc f: [1;3]\rightarrow \R; f(\xi) = \frac{1}{\xi},~f\in C^2([1;3]).

Il vient f''(\xi) = \frac{2}{t^3} et ||f''||_\infty = 2 = M

On cherche donc n \in \N tel que |S_n -\ln(3) | \leq 10^{-2}

Or on sait que |S_n -\ln(3) | \leq 2.\frac{2^3}{24n^2}.

Donc on cherche n tel que 2.\frac{2^3}{24n^2} \leq 10^{-2}. On peut prendre n = 9.

Posté par
maths19re : Riemann 17-03-18 à 12:50

du coup

| ln3 - (\frac{3-1}{2} f(\frac{3+1}{2} |≤  2.\frac{2^3}{24.9^2}

=> Ln(3) ≤ \frac{16}{1944} +1
=> Ln(3) ≤  1,0082.....  avec n =9

or ln 3 = 1,09861 ≥ 1,0082 et pas 1,09861 ≤ 1,0082

Posté par
maths19re : Riemann 17-03-18 à 23:02

donc je ne pense pas que j'ai bon :/

Posté par
jsvdbre : Riemann 17-03-18 à 23:42

Il faut voir quels sont les m_k (définis ici : Riemann )

Ici, a= 1, b=3, donc b-a = 2 et on découpe [1;3] en 9 intervalles de longueur 2/9

m_1 = 1+ 1/9

m_k = m_1 + (k-1)\frac{2}{9},~k\in \{2,\cdots,9\}

Et on devrait avoir \ln(3) \sim \frac{2}{9}\sum_{k=1}^{9}{\frac{1}{m_k}}

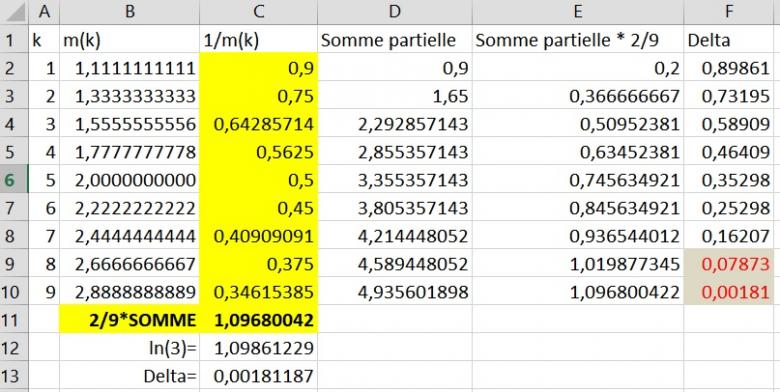
Ci-dessous une simulation avec excel 2013.
La cellule F9 montre clairement que prendre n = 9 est obligatoire pour obtenir la précision voulue.
Et qu'en prenant, n = 9, la précision passe de 8.10^{-2} à 2.10^{-3}

Riemann

Posté par
Axelensre : Riemann 19-03-18 à 21:32

Bonjour, quelqu'un pourrait t-il m'aider pour la question 1) en prenant Sk= frac{b-a}{n}*k

Posté par
Axelensre : Riemann 19-03-18 à 21:40

désolé pour le multi-post  mais j'ai un peu fail ^^

Car quand je remplace Sk et Sk+1 par leur valeur, j'obtiens: \frac{b-a}{n}\sum{ a+(k+\frac{1}{2})\frac{b-a}{n}}   pour k allant de 1 à n
Or le 1/2 est en trop :/

Posté par
jsvdbre : Riemann 19-03-18 à 22:56

Bonjour Axelens.
Non, ce n'est pas du multi-post puisque tu n'ouvres pas deux fils pour une même question

Axelens @ 19-03-2018 à 21:40

quand je remplace Sk et Sk+1 par leur valeur, j'obtiens: \frac{b-a}{n}\sum{ a+(k+\frac{1}{2})\frac{b-a}{n}}   pour k allant de 1 à n

Ce n'est pas possible. Il manque sous ta somme une expression de f.

S_{k}= \frac{b-a}{k} \sum_{i=0}^{k-1} f(\frac{s_i+s_{i+1}}{2})   donc :

S_{k+1}= \frac{b-a}{k+1} \sum_{i=0}^{k} f(\frac{s_i+s_{i+1}}{2})  

Posté par
Axelensre : Riemann 20-03-18 à 16:27

D'accord

En fait quand je pars de \frac{b-a}{n}\sum{f(a+(k+\frac{1}{2})\frac{b-a}{n}}
    pour k allant de 0 à n-1
J'obtiens:


\frac{b-a}{n}\sum{f(a+(k+\frac{1}{2})\frac{b-a}{n}} )     pour k allant de 0 à n-1

Mais pour pouvoir appliquer la formule de Riemann, je ne devrai pas avoir ce 1/2

Posté par
jsvdbre : Riemann 20-03-18 à 17:48

Ça n'a pas d'importance : regarde ce message Riemann

Posté par
Axelensre : Riemann 20-03-18 à 18:00

Donc en quelque dorte le 1/2 est "négligeable"?

Posté par
jsvdbre : Riemann 20-03-18 à 21:23

Ah non, ce n'est pas du tout cela que je dis dans ce message.
Je dis simplement que si tu considères les subdivisions successives de l'intervalle [a;b], alors quelles que soient les valeurs que tu prennes dans les intervalles d'une subdivision, la suite des sommes de Riemann associées à ces subdivisions tendront vers l'intégrale de f.
En particulier, le milieu des intervalles de la subdivision convient.


Rechercher
Menu
Espace membre
Changer d'île

Vous devez être membre accéder à ce service...

Pas encore inscrit ?

1 compte par personne, multi-compte interdit !

Ou identifiez-vous :

Rester sur la page

Inscription gratuite

Fiches en rapport

parmi 1675 fiches de maths

Désolé, votre version d'Internet Explorer est plus que périmée ! Merci de le mettre à jour ou de télécharger Firefox ou Google Chrome pour utiliser le site. Votre ordinateur vous remerciera !