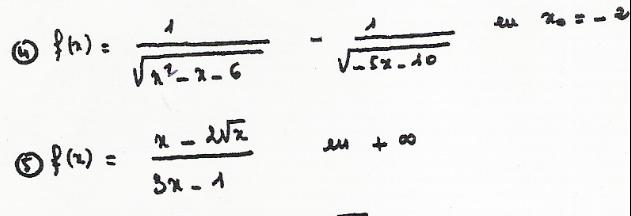Inscription / Connexion Nouveau Sujet
salut Redman 
:
Elle est pas mal ta méthode. mais ce que tu peux aussi dire à infophile quand il a comme ça un quotient de pôlynôme c'est que :
la limite en l'infinie d'un quatient de polynône est égal au terme de au quotient des termes de plus haut degré de chaque polynômes. D'où :
enfin, de toute façon ça revient au m^^eme mais bon ... 
Allez @+ sur l'
!
je recommence :
la limite en l'infini d'un quotient de polynône est égal au quotient des termes de plus haut degré de chaque polynômes
escusez moi pour les fautes de frappes 
salut otto :
je ne crois pas savoir le démontrer, mais ce que je sais c'est que ça marche à tout les coups ( 100% certains ) :
Va voir ici :
@+ sur l
Oui je sais que ca marche, mais si tu ne sais pas démontrer une méthode, évite de l'utiliser, c'est un conseil, ca risque de te faire défaut (notamment face à jury)
Ici la méthode la plus simple pour le montrer c'est justement celle de redman.
Sinon un truc qui est bon à savoir aussi, c'est que si tu as une limite du type f/g f->0 et g->0, alors la limite est celle de f'(0)/g'(0) lorsque f et g sont dérivables à dérivée continue.
Avec un peu de travail, on peut montrer que c'est encore valable en l'infini.
Exemple :
sin(x)/x
sin'=cos
id'=1
donc la limite de sin(x)/x en 0 c'est cos(0)/1=1/1=1
A+
Re
En fait oui, je sais le démontrer à partir de la factorisation par le terme de plus haut degré, mais moi je pensais quand tu m'as dis :
" comment démontres tu ce résultat ? " a chercher une autre méthode ...
Sinon, la propriéter que tu viens de ma citer ensuite, ce n'est pas là le théorème de l'hospital ?
Je l'ai déjà vu utiliser sur ce site, c'est pourquoi je te poses la question !
théorème utilis ici : limites avec ln ou encore ici : Dérivée d une fonction en 0
le problème c'est que moi, je ne l'ai pas vu en cours. As-ton avis, je peux l'utiliser au bac si je suis réelemtn bloqué ?
Oui c'est la règle de l'hôpital.
Tu peux ainsi montrer par exemple que
sin(x)/pn(x) -> 1
Avec pn(x)=x-x^3/3!+x^5/5!+...+(-n)^nx^(2n+1)/(2n+1)!
En réalité on a même un peu mieux que çà...
Notamment la différence entre le sinus et pn est inférieur à 1/(2n+2)!.
A+
Je te déconseille très fortement de l'utiliser au bac.
Normalement, si tu l'as pas vu, c'est que l'examen sera fait pour que tu n'ais pas à l'utiliser.
En revanche tu peux l'utiliser sur ton brouillon, pour avoir une idée du résultat.
Cependant je ne suis jamais très "chaud" pour ce genre d'idée, parce que quelque chose non vu en cours peut etre mal utilisé.
ok merci pour ta réponse -> c'est vrai que ça peut aider à vérifier !
cependant, comme tu le dis si bien : à prendre avec précautions !
@+
N'oubliez pas qu'a la base nous nous adressons à des élèves de 2de qui commencent a apprendre les limites, donc je pense qu'il est mieux pour eux de faire la méthode de factorisation, non?
c'est une méthode qui marche à tous les coups pour une fonction rationnelle.
$
Je n'ai pas très bien compris le théorème de l'hopital,
est ce que c'est celui qui consiste à utiliser le nombre dérivé?
ex : pour
on detérmine la fonction f définie par
et
or
or
donc
si c'est ca, comment on fait à l'infini?
Salut, non ce n'est pas tout à fait çà la règle de l'hôpital.(c'est un cas particulier que tu utilises)
Je l'ai énoncée plus haut, relis la.
A+
je suis d'accord avec otto, c'est pas du tout cas la règle de l'hôpital. Ici tu n'utilises qu'un cas particulier de cette règle
mettons que tu dois étudier cette limite :
en posant et
la règle dis que ( pour des fonctions continues et dérivables ce qui est le cas ) :
@+
Oui attention tout de même, il faut que g et f ne s'annulent pas au voisinage du point pour lequel tu calcules la limite.
Je suis un fervent adepte de la règle du Marquis (celui de LHospital), cependant il ne faut l'employer qu'à bon escient.
De plus, comme elle n'est pas étudiée même en terminale, elle est intrerdite d'utilisation dans les exercicse proposés jusqu'à ce niveau au moins.
Pour pouvoir appliquer la règle du Marquis, il faut entre autres que chacune des fonctions f(x) et g(x) soit dérivable pour la valeur de x pour laquelle la limite est cherchée mais aussi il est impératif d'avoir au départ une des formes indéterminées 0/0 ou oo/oo (quels que soient les signes des oo).
Bonjour,
Auriez vous un autre calcul de limite du meme genre (voir celle de redman le dernier post du precedent topic 
?
Merci d'avance
Sticky
Bonjour tout le monde
Je ne savais pas que vous aviez crée un autre topic ! Merci beaucoup ! 
Oui je vais deja m'entrainer sur les limites, et je rejoins ce que demande Sticky 
Kevin
Pour celle de lyonnais:
x^3 --> +oo
2 --> 2
3/x --> 0
5/x^3 --> 0
------------
x² --> +oo
4 --> 4
7/x² --> 0
------------
x^3 / x^2 = x
et par sommation on a: 2/4 soit 1/2
Or x tend également vers l'infini, donc le tout tend vers l'infini.
C'est ca ?
Pour celle de Redman:
Alors :
Le premier terme avec la grande racine tendra vers +oo mais sur .
On a donc la forme indéterminée:
Le tout tend vers 0 , c'est ca ?
Ensuite pour le document scanné, je ne sais pas par quoi tend x ? 
Enfin pouvez-vous deja me corriger celles que j'ai faites ?
Non surtout pas!!!
quand tu as oo - oo ca ne fait pas 0!
tu as une forme indeterminée
il faut se débrouiller pr trouver une forme déterminée!
(PS: essaie tt d'abord de multiplier et diviser par la la forme conjuguée)
pr celle de lyonnais c'est bon
infophile !
>> Redman :
c'est normal que tu ne vois pas, j'ai mis ma réponse en latex blanc !
il faut que tu surligne la zone et tu vérras ma réponse ...
je te la remet ici si tu veux :
lyonnais
surligne dans mon précédent message la partie en pointillée
je te la remet ici si tu veux :
............
............
............
lyonnais
c'est pa possible que tu ne vois rien !
ok ( je ne voulais juste pas donner la réponse à infophile pour qu'il cherche ... )
j'obtient donc :
en passant par le conjugué ...
@+
Attend, c'est normale, j'ai fait :
et là je trouve 1
Mais pour ta limite, la réponse est 1/2
voila, faut que j'y aille ...
@+
Redman>>
(PS: essaie tt d'abord de multiplier et diviser par la la forme conjuguée)
Comme ca?
Sticky
merci 
et désolé pour l'ambiguité, j'avais calculer l'autre limite lol 
comme quoi je lis bien les énoncés ! Allez, @+
heu, la derniere racine de x au dénomintauer n'était pas sensé etre comprise dans la grande :s
Sticky
Annuler
connectez vous