Annuler
connectez vous
en post-bac
- Équations différentielles : un Cours complet avec des exemples
- Généralités sur les matrices, applications linéaires, changement de base, rang d'une matrice - supérieur
- Ensemble et application Partie II
- Espaces vectoriels et Applications linéaires - supérieur
- Un best-of d'exos de probabilités (après le bac)
Inscription / Connexion Nouveau Sujet
Accueil l'île des mathématiques Forum de mathématiquesListe de tous les forums de mathématiques SupérieurOn parle exclusivement de maths, pour le supérieur principalement, les BTS, IUT, prépas... Reprise d'études [tout]Lister tous les topics de mathématiques
Niveau Reprise d'études
Translation
Posté par 
Ramanujan
RamanujanBonjour,
Mon sujet CAPES a atteint le maximum de post possible. J'ai bien avancé mais je bloque à la question suivante.
On rappelle que est le groupe des isométries affines
de
telles que
Soit la translation de vecteur
. Montrer que
si et seulement si
=> Soit . Alors
est une isométrie affine qui vérifie
Je comprends pas pourquoi il faut montrer qu'un vecteur appartiennent au groupe des isométries pour moi ça n'a pas de sens 
malou edit > ceci est la suite de 
CAPES maths 1 2017
Ah 
=>
Soit alors :
donc
Or
On a montré la première implication.
<=
Soit
Il faut montrer que soit que
Montrons
Soit
Alors
On a montré
Enfin montrons :
Soit je dois montrer qu'il existe un
tel que :
Il suffit de prendre alors
L'équivalence est démontrée 
Soit f un élément de G et t' la translation de vecteur . Montrer que t' est élément de G et que
est un élément de
donc
donc
D'après la question précédente cela implique que
Je veux montrer que
Je bloque ici : je vois pas comment continuer.
Je bloque à la dernière question de cette partie :
Montrer que tout élément de
s'écrit de façon unique
avec
translation de vecteur dans
et
élément de
comme on ne sait pas qui est G0, on ne risque pas de pouvoir t'aider !
tes énoncés sont toujours aussi incomplets et fouillis !
ensuite ce n'est pas très dur de montrer qu'en supposant qu'il y a deux décompositions, les deux translations sont égales... et que donc les deux fonctions g aussi
matheuxmatou @ 22-11-2018 à 23:38
ben alors tu as déjà montré l'existence en utilisant la question précédente ...
ben alors tu as déjà montré l'existence en utilisant la question précédente ...
J'ai pas compris le rapport avec la question précédente où j'ai :
Et là je dois montrer qu'il existe
Je vois pas le lien entre les 2 égalités
ah ben faut quand même faire un effort !
compose dans les deux membres à gauche par la translation de vecteur f(O)
à titre indicatif je te ferait remarquer que c'est la réciproque de t' 
Ah oui merci pour votre aide
Soit la translation de vecteur
et
la translation de vecteur
Alors :
Composons par on obtient :
La composition d'applications linéaires étant associative :
On a montré :
Or est une translation de vecteur
car
Et d'après la question précédente.
Unicité :
Soit :
Comme alors
De même pour
Donc
D'où ce sont les translations de vecteur
Toute application affine étant bijective existe et :
On a montré l'unicité.
Bonjour !
Tu es un vrai champion !
Manipuler des groupes et des matrices et demander après plus de 150 posts si l'opération est associative !
Et si un farceur te répond "non", tu recommences le tout ?
Bah je savais que le produit de matrice était associatif et la composition des applications j'avais oublié
Je suis à la partie D.
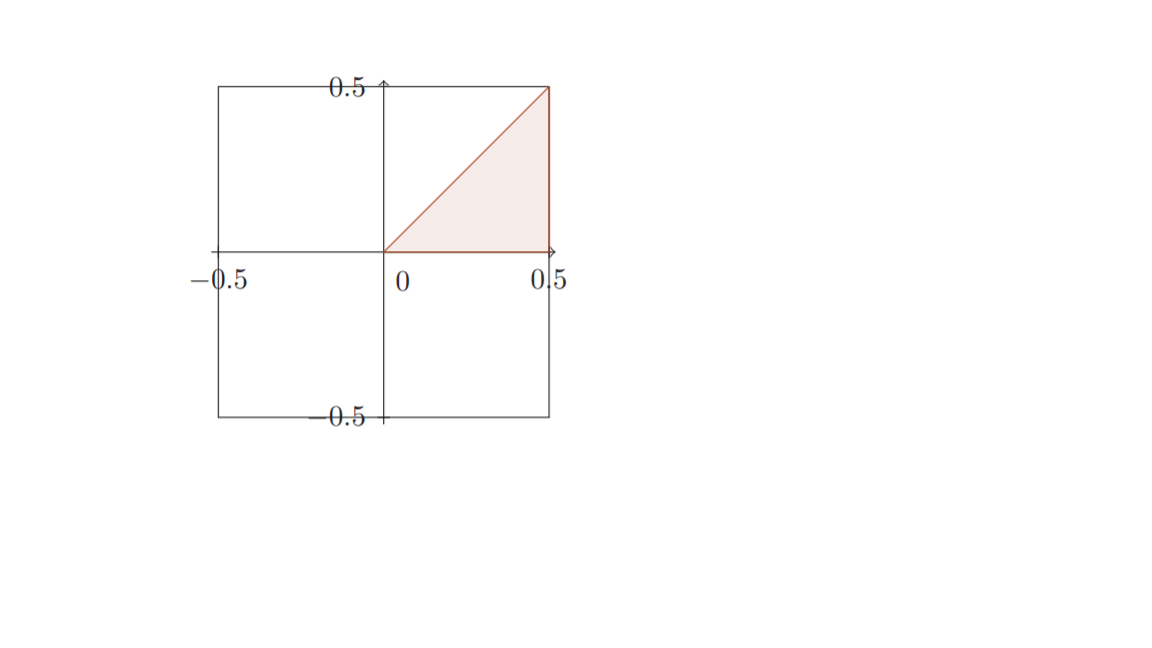
Soit la surface délimitée par le triangle de
dessiné en rouge. Soit
la carré dessiné ci-dessous.
Justifier que
Je vois pas comment faire.
J'ai démontré que les éléments de sont :
L'identité, la symétrie orthogonale d'axe , la symétrie orthogonale d'axe
, la symétrie centrale de centre O, la symétrie orthogonale d'axe
, la rotation de centre O et d'angle
, la rotation de centre O et d'angle
et la symétrie orthogonale d'axe
Je dois procéder par double inclusion ?
En fait, j'ai l'idée mais je sais pas comment rédiger. On peut reconstruire le carré à partir du triangle rouge en utilisant tous les isométries affines de mais je sais pas comment le traduire mathématiquement.
Tu prends ton carré tu numérotes tes sections et tu assignes à chaque numéro la transformation correspondante, pas besoin de faire du calcul différentiel pour démontrer ça, un dessin suffit
Je vois mais d'habitude pour démonter une égalité d'ensemble on procède par double inclusion.
Ici c'est différent ?
Tu sais tu peux aussi montrer que a=b en montrant que
et
mais est ce que ca a toujours un interet?...
Bah non en effet.
Identité de
On obtient par symétrie orthogonale d'axe
de
On obtient par symétrie orthogonale d'axe
de
On obtient par symétrie centrale de centre
de
On obtient par symétrie orthogonale d'axe
de
On obtient par rotation de centre
et d'angle
de
On obtient par rotation de centre
et d'angle
de
On obtient par symétrie orthogonale d'axe
de
On a reconstruit le carré en faisant l'image de
par tous les éléments de
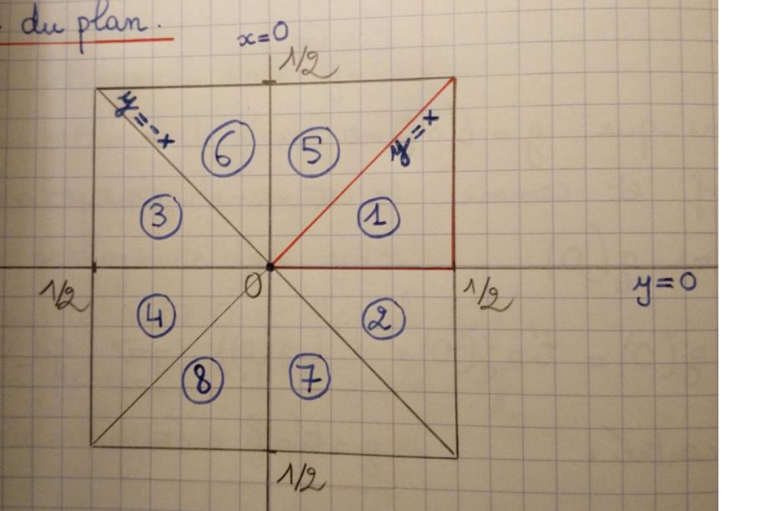
Montrer que si et
sont 2 éléments distincts de
alors
est soit un segment soit un point.
C'est facile à voir sur le dessin, mais je vois pas comment le démontrer en général.
Je suis d'accord pour le début.
Mais je comprends pas : "il suffit de chercher les points de dont l'image par un
sont encore dans
"
Il faut trouver les points tels que :
. Je vois pas comment faire.
Tu connais les éléments de .
Pour chacun d'eux tu cherches les points de dont l'image est encore dans
.
Évidemment ce serait plus simple si tu avais écrit la liste des éléments de de manière claire : par exemple
pour les symétries axiales,
pour les rotations.
Chercher les points tels que
est alors facile : 8 vérifications à faire.
Ok je vais les écrire sous la forme et
Mais j'ai pas compris le rapport entre ce qu'on cherchait au départ :
Les points tels que
et
tels que
Et c'est quoi par rapport à
et
?
Ah en fait j'ai compris !
car
est un groupe.
Mais il y a que 7 vérifications à faire non ? Vu que alors
?
L'identité est exclue sinon on aurait ni un point ni un segment.
Si est la symétrie orthogonale d'axe
on cherche les points de l'ensemble :
est le triangle de sommets
Donc est un segment.
Mais ceci est-il une démonstration ? J'ai juste fait un dessin.
Je trouve que pour les symétries orthogonale d'axe ,
,
et
c'est un segment. Ce segment est le segment commun au triangle
et son image par ces symétries.
Pour la symétrie centrale de centre O je trouve que c'est un point
Pour les rotations de centre O c'est aussi un point
L'identité est exclu car
Après je me demandais, même si c'est pas demandé ici, comment faire pour démontrer que par exemple :
de sommets
,
et
Et de sommets
,
et
S'intersectent en
Quelle est la méthode ?
Tu ne sais donc pas écrire la relation définissant un demi-plan ?
Si la frontière a pour équation l'un des demi-plans vérifie
.
Et n'est que l'intersection de trois demi-plans !
Ah d'accord, j'avais jamais vu ça sous cet angle. Mais j'ai compris le principe.
Je suis habitué à écrire les droites sous la forme :
Pour ma suite du problème encore une question qui semble évidente mais je vois pas comment le démontrer.
, on note
la translation de vecteur X. Justifier que :
Comme d'habitude !
Citation :
Je suis habitué à écrire
et tu perds toutes les parallèles à l'axe des ordonnées, pas très malin !
Je suis habitué à écrire
..................................................................
Une égalité de deux ensembles ? Deux inclusions à établir !
Prends un point
L'autre inclusion étant évidente...
J'arrive pas à traduire en équation.
Je prends :
Et je note la translation de vecteur
Et là je bloque.
C'est quand même pas compliqué de voir qu'un point est dans C s'il a ses deux coordonnées entre -1/2 et 1/2, si ?
Et pour t'éviter de "bloquer" encore, ajouter des entiers convenables à pour arriver à ce que suggère lafol (bonsoir!) devrait être à ta portée !
tu arrives pas à piger qu'en se déplaçant d'une unité à la fois, on devra forcément passer dans un intervalle de largeur 1 ?
Et si tu cherchais des entiers tels que
.
En cherchant bien dans tes souvenirs ? Du côté de la notion de "partie entière" ?
Je trouve comme condition :
Ainsi :
Ainsi on reconnait l'inégalité de la partie entière et on a forcément :
et
C'est juste ?
Citation :
Je trouve pas la même chose que vous :
Je trouve pas la même chose que vous :
C'est nouveau, ça vient de sortir ! (Coluche)
Quand
.......................................................
Citation :
et on a forcément :
Faux ! Réfléchis un peu !et on a forcément :
Bah j'ai pris au départ et
Je comprends pas l'erreur car :
Tout nombre réel est compris entre sa partie entière et sa partie entière + 1 .