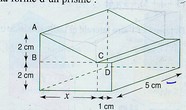
Bonjour,

Théo a bien calculé pour x = 3 ; le résultat est bien 55 cm³

Ce n'est pas plus difficile pout la deuxième question, elle se fait exactement de la même manière
Au lieu d'avoir pour le parallélépipède rectangle
(3 + 1) * 2 * 5 = 40 cm³
on a
(x + 1) * 2 * 5 = 10 * (x + 1) cm³

Pour le prisme à base triangulaire posé sur le parallélépipéde, on avait pour la première question :
(1/2) * 3 * 2 * 5 = 15 cm³

et on a pour la deuxième question :
(1/2) * x * 2 * 5 = 5 x cm³

Au total :
10 + 15 x cm³

merci Coll
mais pourquoi au total 10 + 15x cm3
je ne comprends pas très bien  pourquoi pas 10 + 5 x cm3

et pour le tableau en dessous théo doit convertir BC en cm (O) en volume en cm3 je ne comprends pas....

merci encore   la maman de théo

encore un problème a résoudre pour demain

Elle désire vernir l'extérieur du coffre (y compris le dessous) pour cela elle achère une boite de vernis. La boite est remplie au 3/4 et 1 L de vernis couvre 14m2. Quel est le volume de la boite ? a -telle assez de vernis pour passer 2 couches .
théo a répondu a la 1ère question : 3.14 * 8 *10 = 251 cm3 251 * 3/4 = 188 cm3   j'ai un doute  mais bon....

merci pour la personne qui peut nous aider

Bonjour,

Merci de respecter les règles du forum, et de créer un nouveau fil pour ce nouveau sujet.

Nicolas

excusez moi
c'est la première fois que je me sers du forum donc je ferais attention maintenant  merci
la maman de théo

Pas de souci.

Nicolas

est ce que quelqu'un peut nous aider !!!!!
merci

Je reprends les questions du message de 17 h 18

Le volume total est la somme du volume du parallélépipède rectangle : cm³
et du volume du prisme à base triangulaire cm³

Donc le volume total est :
= = cm³

Pour le tableau, il faut remplacer x par les différentes valeurs qu'il peut prendre : 0 ou 1 ou 2 ... ou 5 et calculer à chaque fois le volume, c'est-à-dire calculer à chaque fois 10 + 15x

Par exemple pour x = 3 on retrouve le résultat de la première question puisque 10 + 15x = 10 + (15 * 3) = 10 + 45 = 55 cm³

merci
pour le tableau théo a trouvé la même réponse que vous
merci encore pour votre aide

Et le coffre avec son vernis ? Résolu ?

bonsoir à tous!

excusez-moi pour l'interruption...

Coll> pourrais-tu apporter une explication plus pointue sur ce sujet, stp? (si tu as le temps)

merci d'avance!

oups le lien:
(Lien cassé)

Pour le coffre : le volume du cylindre n'est pas correct (et donc le volume de vernis ne l'est pas non plus).
La surface d'un disque de rayon R = 4 cm est S = .R² = .4² = .16 cm²

Quelle est la surface du coffre ?

Ce que je trouve :
Volume de la boîte : 160. 503 cm³
Volume de vernis 377 cm³ c'est-à-dire de quoi couvrir une surface de 5,28 m²
Surface du coffre 3,425 m²
Il n'y a pas assez de vernis pour 2 couches.

Merci par avance de me dire si vous ne trouvez pas cela.