Annuler
connectez vous
logique en post-bac
- Description de mathématique formelle-termes et relations
- Théorèmes
- Théories logiques
- Équations différentielles : un Cours complet avec des exemples
- Généralités sur les matrices, applications linéaires, changement de base, rang d'une matrice - supérieur
- Ensemble et application Partie II
- Espaces vectoriels et Applications linéaires - supérieur
- Un best-of d'exos de probabilités (après le bac)
Inscription / Connexion Nouveau Sujet
Accueil l'île des mathématiques Forum de mathématiquesListe de tous les forums de mathématiques SupérieurOn parle exclusivement de maths, pour le supérieur principalement, les BTS, IUT, prépas... Autre LogiqueTopics traitant de logique [tout]Lister tous les topics de mathématiques
Niveau autre
Diagramme commutatif?
Posté par Fractal
Bonjour 
Quelle est la définition précise d'un diagramme commutatif (en théorie des catégories).
La définition de Wikipédia dit que si on prend deux objets quelconques et deux chemins quelconques qui relient l'un à l'autre, alors les composées seront les mêmes.
Mais dans ce cas que dire de ce genre de diagramme :
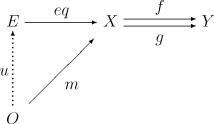
J'aurais tendance à penser que pour aller de X à Y on peut soit passer par f, soit par g, donc que f = g, mais ce n'est évidemment pas ce qu'il signifie sinon il n'y aurait qu'une seule flèche (je sais ce que veut dire ce diagramme, là n'est pas ma question, c'est juste pour dire que la définition ne me semble pas vraiment claire)
De même, est-ce que si un diagramme fait une boucle on peut considérer que la composée des flèches vaut la flèche identité? (vu que quand on ne bouge pas c'est comme si on avait suivi la flèche identité)
Enfin, est-ce que les raisonnements à base de diagrammes commutatifs sont légitimes? Auriez-vous un document ou quelque chose qui expliquerait en quoi un diagramme commutatif est une preuve (pourquoi quand on regroupe plusieurs diagrammes commutatifs il reste commutatif, pourquoi de rajouter une flèche à un endroit ne risque pas de "casser" la commutativité ailleurs, etc.)
Merci
Fractal 
Bonjour Fractal
Dans le diagramme ci-dessus la commutativité signifie
m=eq o u, f o eq=g o eq et ce que l'on en déduit. Il ne faut pas imposer des commutativités avec l'identité. Dans ton diagramme (qui définit le noyau d'une double flèche par propriété universelle) bien sur f et g ne sont pas supposés égaux.
Si tu veux un peu de théorie des catégories je peux te signaler des très vieux bouquins (ce sont les originaux et c'est là que j'ai appris...)
Mitchell: Theory of categories
Cartan & Eilenberg: Homological algebra
Spanier: Algebraic topology (celui-ci dirigé vers la topologie mais contenant les définitions de base)
Si ça t'intéresse, je peux rechercher mieux les éditeurs et l'année (ils sont sur une étagère haute!)
Bonjour Camélia
Oui oui, je sais ce que signifie ce diagramme, mais j'aimerais comprendre pourquoi est-ce qu'il faut le comprendre ainsi.
Il me semble que la définition de Wikipédia ne colle pas, à moins peut-être que l'on impose qu'il y ait au moins deux flèches entre les deux objets considérés.
J'ai l'impression (mais je peux tout à fait me tromper) que les diagrammes commutatifs ne sont pas seulement une aide à la réflexion, mais peuvent constituer véritablement une démonstration en eux-mêmes (par exemple pour montrer qu'un graphe est planaire un dessin suffit, et constitue, il me semble, une démonstration parfaitement rigoureuse, du moment qu'il n'y a pas d'ambiguité sur ce qui est dessiné).
Par exemple pour montrer que deux objets initiaux sont isomorphes, on peut le faire avec des mots :
Citation :
Si e et e' sont initiaux, il existe f : e -> e' et g : e' -> e, d'où fog : e' -> e' et gof : e -> e, mais e et e' étant initiaux il n'existe qu'une seule flèche e -> e qui est l'identité de e, d'où gof = ie et de même il n'existe qu'une seule flèche e' -> e' qui est l'identité de e', d'où fog = ie'.
Par conséquent f et g sont des isomorphismes, donc e et e' sont isomorphes.
Si e et e' sont initiaux, il existe f : e -> e' et g : e' -> e, d'où fog : e' -> e' et gof : e -> e, mais e et e' étant initiaux il n'existe qu'une seule flèche e -> e qui est l'identité de e, d'où gof = ie et de même il n'existe qu'une seule flèche e' -> e' qui est l'identité de e', d'où fog = ie'.
Par conséquent f et g sont des isomorphismes, donc e et e' sont isomorphes.
Mais on pourrait aussi faire un diagramme avec e et e', ainsi que les flèches f, g, ie et ie' en pointillés (pour dire qu'elles sont uniques), et il contient exactement les mêmes informations que la démonstration avec des mots (on a l'existence des flèches, et leur composition donne des flèches e -> e et e' -> e' dont il est indiqué sur le diagramme qu'elles ne peuvent être que l'identité)
Mais a-t-on le droit de faire ce genre de diagramme, et est-ce pour autant une preuve?
En gros ma question est de savoir laquelle de ces deux phrases est vraie :
* Un diagramme commutatif sert à montrer informellement pourquoi une certaine propriété est vraie; une preuve resterait à écrire pour être parfaitement rigoureux mais le diagramme donne quasiment tous les éléments pour.
* Un diagramme est une démonstration absolument rigoureuse qui peut tout à fait remplacer une preuve par des mots (mais dans ce cas il nous faudrait une définition parfaitement rigoureuse d'un diagramme commutatif)
Merci
Fractal
Bonjour
C'est la deuxième phrase qui est vraie. La définition rigoureuse d'un diagramme commutatif n'est pas si commode. C'est du même genre Bourbaki qui espérait réduire les maths à 4 signes...
Je viens de regarder la définition rigoureuse dans Mitchell, j'ai même commencé à la recopier, et j'ai renoncé, car je n'y comprenais pas tout...
Néanmoins, je n'ai jamais été génée pour écrire les diagrammes classiques, produit, produit fibré, limites inductives et leurs co- et la communauté mathématique accepte très bien un diagramme comme démonstration. Pour l'"unicité" de l'objet initial, le diagramme dont tu parles suffit largement!
La deuxième phrase? C'est pas la première que tu voulais dire, plutôt?
Sinon, j'ai une autre question que je me suis souvent posée : quand on voit toute l'axiomatique derrière la théorie des ensembles, comment se fait-il que celle de la théorie des catégorie soit si faible (ou peut-être c'est que je ne l'ai jamais vue)? Une collection c'est quelque chose de vraiment très vague, est-ce que j'ai le droit de considérer la catégorie des catégories par exemple? Ne risque-t-il pas d'y avoir un autre paradoxe de Russel?
Ou bien y a-t-il toute une axiomatique très précise derrière, mais qui ne se trouverait quasiment nulle part?
Encore une petite précision : dans la définition d'une catégorie, Wikipédia parle d'ensemble des morphismes de A vers B; faut-il effectivement que ce soit un ensemble, ou bien juste une collection? (il me semblerait bizarre qu'il faille la notion d'ensemble pour définir une catégorie, et j'ai d'ailleurs un livre qui parle bien de collection de flèches)
Fractal
Bonjour fractal
Je pense que tu mérites mieux qu'une réponse dilatoire et j'ai été moi-même véxée de ne pas pouvoir expliciter un "détail" d'un domaine qui me tient à coeur.
D'ailleurs je suis ravie que des jeunes s'y intéressent.
Alors voilà: explications tirées de "Categories for the Working Mathematician" de Saunders Mac Lane (Springer-Verlag 1971) que je ne saurais pas trop te recommander.
Il n'y a aucun doute: dans un diagramme commutatif, il y a une et une seule flèche qui va d'un objet à un autre. En particulier, pas de boucle, d'un objet dans lui-même il n'y a que son identité.
Et alors? ton diagramme n'est pas un diagramme commutatif! Voici la construction du conoyau d'une double flèche (et la plupart des limites projectives se font sur le même modèle).
On commence par définir une "flèche universelle" de la manière suivante:
Si est un foncteur et si c est un objet de C, une flèche universelle de c vers S est un couple < r,u > formé d'un objet r de D et d'une flèche u:c
S(r) dans C telle que pour tout couple < d,f > formé d'un objet d de D et d'une flèche f:cS(d) il existe une et une seule flèche f':r d telle que S(f') o u=f.
Bien sur, c'est maintenant qu'il faut montrer que deux flèches universelles pour la même situation sont isomorphes.
On revient aux conoyaux! (co, car je n'ose renverser toutes les flèches en tappant!)
Soit la catégorie formée d'exactement deux objets (avec leurs identités) et de deux flèches allant du premier vers le second.
Considérons la catégorie des foncteurs de
vers C. Un objet de
est donc une double flèche (f,g) allant d'un objet a vers un objet b dans C. Une flèche de
est une transformation naturelle (h,k) entre deux foncteurs, voilà le diagramme: les deux lignes sont les deux objets, la flèche est en vertical:
tels que kf=f'h et kg=g'h.
De plus, à un objet c de C on associe la double flèche et à une flèche
de C on associe
l'élément de
qui avec les notations ci-dessus vaut =b=a'=b'=c, f=f'=g=g'=1c et h=k=r. Ceci définit un foncteur
Je te laisse le plaisir de vérifier que la donnée de flèches f et g de a dans b et d'une flèche h de b dans c telles que hf=hg (un coégalisateur) est la même chose que la donnée de la flèche verticale (hf,h) de l'objet double flèche (f,g) dans vers
et que
le conoyau vérifie la propriété universelle au sens donné ci-dessus.
OUF! Morale: il est bon de l'avoir vu une fois, mais il ne faut pas en abuser...
Réponse à tes nouvelles questions (tu es doué pour mettre le doigt sur les difficultés). De mon temps il était essentiel que les flèches entre deux objets forment un ensemble. En revanche, il y avait du laxisme sur "tous" les objets. Il y a eu des tentatives de définition de trucs appelés univers, qui avaient les mêmes ennuis que les ensembles. Un temps on a prétendu imposer que les classes d'isomorphisme des objets forment un ensemble. En fait, on a plus ou moins renoncé à légiférer comptant sur le bon sens des spécialistes. En réalité, on ne travaille que rarement avec tous les ensembles, ou tous les groupes...
Il vaut mieux éviter de parler de la catégorie des catégories, ne serait-ce que parce que les foncteurs d'une catégorie dans une autre ne forment pas un ensemble, mais on fait comme si ...