Inscription / Connexion Nouveau Sujet
Relation binaire
Bonsoir,
Je ne comprends pas la définition d'une relation binaire donnée dans mon cours surtout la partie en vert.
Soit E un ensemble.
On appelle relation binaire sur E toute application de
dans
.
On dit que x est en relation avec y lorsque ce que l'on note
.
L'ensemble des éléments de
tels que
s'appelle le graphe de
.
Donc peut être égal à 0 ? Ca veut dire que
? Ca veut dire quoi
?
Merci.
Salut. On peut avoir plusieurs définitions de "relation binaire", mais on s'y retrouve facilement. On peut voir une relation binaire comme un symbole de proposition, un graphe, ou bien comme une application de dans
, qui fait office d'ensemble
.
Quand on a ça veut dire que x et y sont en relation par R, si par contre
ils ne sont pas en relation.
R est définie comme une application de dans
donc oui à priori
peut valoir 0 ou 1 mais pas les deux à la fois ...
Et ben ssi x et y ne sont pas en relations .
Par exemple , peut-tu expliciter R pour la relation d?égalité dans E ? Celle où tout le monde est en relation avec tout le monde ?
@SkyMtn
Ok ça marche !
@Zrun
Pas compris. J'arrive pas à saisir comment on la trouve la relation R à partir de la définition.
Bonsoir
tes questions n'ont aucun sens...
tu n'as toujours pas compris ce qu'est un ensemble, ce qu'est une partie d'un ensemble, ce que sont des éléments d'un ensemble, la différence entre "être une partie de " et "être un élément de " etc
il n'y a que deux exemples possibles de R(x,y) =, comme tu dis ! R(x,y) = 0 ou R(x,y) = 1 !
Si je sais ce que c'est un ensemble et comment déterminer ses parties.
J'ai pas compris c'est quoi le je trouve la définition incompréhensible.
D'après le cours :
est définie comme une partie de
:
lorsque (x,y) appartient à ce graphe.
Exemple :
La droite d'équation y=x est bien une partie de et les couples (x,y) appartiennent bien à cette partie qu'on appelle graphe.
bonjour,
R(x,y)=1 veut dire x et y sont en relation
Cette définition ne me semble pas adéquat car "x et y sont en relation" est une proposition qui est symétrique dans le langage courant.
.Le couple (x,y) n'est pas égal au couple (y,x)
or on peut avoir R(x,y)=1 et R(y,x)=0 si R n'est pas symétique.
exemple: " x divise y "dans un ensemble d'entiers ex E= {2,3,4,5,6} R(2,6)=1; R(6,2)=0
Cette définition ne me semble pas adéquat car "x et y sont en relation" est une proposition qui est symétrique dans le langage courant.
Et quid de « x est en relation avec y » . En français ça peut sembler symétrique mais c'est la traduction exacte de
salut
DOMOREA a donnée une bonne idée ...
soit R la relation R(x, y) = 1 <=> x divise y
Ramanujan : peux-tu donner le graphe de R dans l'ensemble E = {0, 1, 2, 3, 4, 5, 6, 7, 8, 9, 10} ?
Cette définition ne me semble pas adéquat car "x et y sont en relation" est une proposition qui est symétrique dans le langage courant.
Et quid de « x est en relation avec y » . En français ça peut sembler symétrique mais c'est la traduction exacte de
en français, "x est en relation avec y" ne signifie pas la même chose que "y est en relation avec x", sauf si la relation est symétrique
exemple de relation non symétrique : la vassalité dans l'ensemble des humains vivant au moyen-âge ....
bonjour Lafol,
évidement tout à fait d'accords avec toi mais en écrivant cela je visais une partie de l'intervention de SkyMtn
Quand on a R(x,y)=1 ça veut dire que x et y sont en relation par R
xRy ou x est en relation avec y ne suppose pas la symétrie
en français, "x est en relation avec y" ne signifie pas la même chose que "y est en relation avec x", sauf si la relation est symétrique
exemple de relation non symétrique : la vassalité dans l'ensemble des humains vivant au moyen-âge ....
Je sais ce qu'est une relation (non)symétrique ... Et en français purement linguistique (en sortant de notre vision mathématique) si « A est B » alors « B est A » par exemple « Tom est blanc » et « Blanc est Tom » ... je dis juste que si on demande à une personne n'ayant pas fais d'étude sur les relations d'ordre , il considérerai que si « x est en relation avec y » alors « y est en relation avec x » ...
Mathématiquement on est tous d'accord que ce n'est pas pareil !
Hum. 
Si je suis blanc alors tous les blancs sont moi.
J'ai comme un doute, même si on sort du cadre mathématique.
je ne suis pas d'accord
ça ne viendrait à l'idée de personne qu'on peut échanger corbeau et noir dans les phrases "ce corbeau est noir" et "ce noir est corbeau" (ou alors ne pas lui faire faire de journalisme ..)
de toutes façons, là, il y a "est en relation avec" et pas "est" qui pourrait être plus ou moins synonyme de "égale", par exemple dans des phrases comme "un sou est un sou"
le "avec" rompt la symétrie, justement : ce n'est pas exactement la même chose de dire "je vais à Paris avec ma sœur", ou "ma sœur vient à Paris avec moi"
Bonjour 
Soit E un ensemble.
On appelle relation binaire
On dit que x est en relation avec y lorsque
Je trouve absurde d'appeler "relation", même si on lui colle le qualificatif de "binaire", un objet mathématique.
Une relation est un lien logique entre des objets mathématiques.
Une application de
Certes, à partir de cet objet, on peut en déduire une relation, mais on ne peut pas confondre les deux notions.
Donc oui,
tes questions n'ont aucun sens...
Simplement parce que l'énoncé est mal formulé ...
Donc relation de cause à effet... et personne n'ira confondre la relation de cause à effet, avec l'effet (ou la cause)

salut
DOMOREA a donnée une bonne idée ...
soit R la relation R(x, y) = 1 <=> x divise y
Ramanujan : peux-tu donner le graphe de R dans l'ensemble E = {0, 1, 2, 3, 4, 5, 6, 7, 8, 9, 10} ?
Je dois trouver des couples de ExE où x divise y donc :
(1,1) , (1,2) , (1,3) , (1,4) , (1,5) , (1,6) , (17) , (1,8) , (1,9) , (1,10) , (5,10) , (3,6) , (2,4) , (2,6) (2,8), (4,8) , (2,10) , (2,2) , (3,3) , (4,4) , (5,5) , (6,6) , (7,7) , (8,8) , (9,9) , (10,10)
Quel fouillis.... Pas étonnant d'en oublier en étant aussi bordélique.... 3 ne divise plus 9 par exemple ?
Y en a tellement que c'est facile d'en oublier.
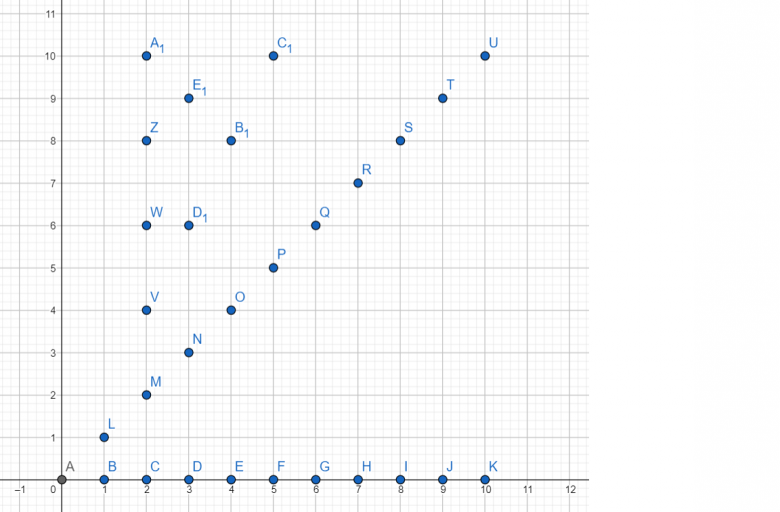
Je vais tracer le graphique des points (x,y) qui vérifient la relation R ça sera plus simple pour ne pas en oublier.
je ne suis pas certain que (0;0) puisse être dans le graphe de cette relation

0 divise bien 0 car il existe un entier (par exemple 1) tel que 0=1*0

Bonsoir,
Soit un ensemble.
Soit une application. Cette application induit sur
une relation binaire définie par
. Remarquons au passage que la fibre
peut être vide. Réciproquement, soit une relation binaire sur
de graphe
(lequel peut être vide !). Alors, cette relation binaire est induite sur
par l'application
qui est uniquement déterminée.
Bonsoir,
Soit
Soit
qui est uniquement déterminée.
Ah j'ai compris maintenant

je ne suis pas certain que (0;0) puisse être dans le graphe de cette relation

0 divise bien 0 car il existe un entier (par exemple 1) tel que 0=1*0

mais la définition de diviseur commence par : un entier non nul n divise l'entier m si ....
0 vérifie bien ce qui suit le si mais pas ce qui précède le si

bonjour,
la définition de "relation" qui a été donnée en début de post et transcrite par Ramanujan est celle donnée par Lucien Chambadal
dans son dictionnaire des mathématiques modernes édité par LAROUSSE
ça va jsvdb ? tout va bien ?

faut pas répondre à une heure pareille ! ....on n'a plus les yeux en face des trous ...

certes ....
mais la définition de diviseur commence par : un entier non nul n divise l'entier m si ....
0 vérifie bien ce qui suit le si mais pas ce qui précède le si

On ne doit pas avoir la même définition de la divisibilité : http://www.animath.fr/IMG/pdf/cours-arith1.pdf page 4 , définition puis les premières remarques qui suivent

![]() Divisibilité - PGCD et PPCM - Nombres premiers et la plupart des définitions sont celles-ci ...
Divisibilité - PGCD et PPCM - Nombres premiers et la plupart des définitions sont celles-ci ...
il est vrai qu'on peut "extrapoler à 0" comme il est dit dans ton lien ... et je le dis toujours oralement ...
mais du point de vue pédagogique je préfère retirer 0 car on voit tant d'élèves écrire la monstruosité 2/0 par exemple ... (par exemple pour les limites en terminale)
Je suis d'accord avec ton point de vue , c'est sur que ça peut embrouiller les élèves !!
Il ne faut pas confondre 0 divise 0 et la fraction 0/0 qui n'a aucun sens . Et ce que je pense ne comprennent pas tous les élèves , c'est qu'il y a le 0 d'analyse (pour les limites) et le 0 d'algèbre ...
Petite question :
Soit R une relation d'équivalence.
Si pourquoi
?
J'ai écris :
par transitivité.
Mais je vois pas comment conclure.
Comme n'importe quelle égalité d'ensembles (parties)...
Soit , alors
, mais comme
on a aussi
et enfin
.
Cela montre et on montrerait de la même manière l'inclusion réciproque

@Ramanujan
Je me souviens du mauvais vieux temps . . .
En cinquième on apprenait ce qu'est une partition d'un ensemble, puis on définissait les relations d'équivalences en disant qu'elles sont associées à une partition.
C'est une image que tu peux retenir.
Avec ta définition d'une relation les couples de R forment des blocs « carrés » le long de la diagonale principale.
ça va jsvdb ? tout va bien ?

faut pas répondre à une heure pareille ! ....on n'a plus les yeux en face des trous ...

Oui, malou, tout va bien, il y a juste qu'après avoir fustigé l'idée qu'une relation, même binaire, n'est pas un objet mathématique, j'aurai dû faire ce qu'a fait ThierryPoma, savoir, dire ce qu'est une relation binaire ... d'où ma réflexion qui a pu paraître bizarre

Comme n'importe quelle égalité d'ensembles (parties)...
Soit
Cela montre

Merci j'ai écrit la démo ça marche nikel.
J'aimerais savoir quelle est la méthode pour déterminer le contraire de cette équivalence :
En fait c'est la symétrie et j'aimerais déterminer l'antisymétrie.
Attention !
La négation de la symétrie c'est , alors que l'antisymétrie c'est
... symétrie et antisymétrie ne sont pas négation l'une de l'autre.
une fonction est une relation binaire ...
R :si alors f est réflexive
S :si alors f est symétrique
A :si alors f est antisymétrique ... mais au fait qu'est ce que cette relation = ?
T :si alors f est transitive
toute fonction vérifiant les propriétés R, S et T est appelée relation d'équivalence
toute fonction vérifiant les propriétés R, A et T est appelée relation d'ordre

ainsi dans muni de sa relation d'ordre naturel la fonction f est définie par :
et la fonction g définie par n'est pas réflexive donc n'est pas une relation d'ordre
cette fonction g est la relation binaire est inférieur strictement
mais il est tout de même plus simple de résumer la suite des six symboles ou
en
ou
la relation binaire définit dans Z la relation d'ordre
n divise m
la relation binaire (d'équivalence) est donnée par la fonction

Je dénie formellement à une fonction, terme mathématique, d'avoir le droit de porter le nom de « relation « .
C'est une antinomie.
C'est comme confondre l'etre Et l'avoir, les torchons et les serviettes.
Il faut que tu reviennes à la définition de l'equivalence
Dans le cours y a que la table de vérité de l'implication.



 algèbre en post-bac
algèbre en post-bac