Annuler
connectez vous
logique en post-bac
- Description de mathématique formelle-termes et relations
- Théorèmes
- Théories logiques
- Équations différentielles : un Cours complet avec des exemples
- Ensemble et application Partie II
- Généralités sur les matrices, applications linéaires, changement de base, rang d'une matrice - supérieur
- Espaces vectoriels et Applications linéaires - supérieur
- Ensemble et application Partie I
Inscription / Connexion Nouveau Sujet
Accueil l'île des mathématiques Forum de mathématiquesListe de tous les forums de mathématiques SupérieurOn parle exclusivement de maths, pour le supérieur principalement, les BTS, IUT, prépas... Maths sup LogiqueTopics traitant de logique [tout]Lister tous les topics de mathématiques
Niveau Maths sup
exercice sur la théorie des ensembles(1)
Posté par hedgefunder
Bonsoir à tous,
j'ai besoin de votre aide pour corriger ma démonstration
exercice:
Soit A,B et C trois ensembles.
(A
B)
(AC) (1) et (A
B)(AC) (2)
que dire de B et C
solution que je propose:
a)soit x
A et xB d'apres (1) xC
b)soit xA ou xB d'apres (2) xA ou xC.
soit xB et x
A (cas particulier de "xA ou xB") alors xC d'apres (2) en effet xA
CCl: Ainsi 
xB ,xC
d'où BC
est-ce rigoureux?
PS: Noflah si tu lis le topic je l'ai fait surtout pour la démonstration (je sais que la conclusion est juste), aussi je vais mettre les autres exos sur le forum quand j'aurai fini de tout rediger.
Merci
Salut pierre 
Tu peux être un peu plus précis dans la démonstration pour le (a) ?
Imagine qu'on a cette configuration :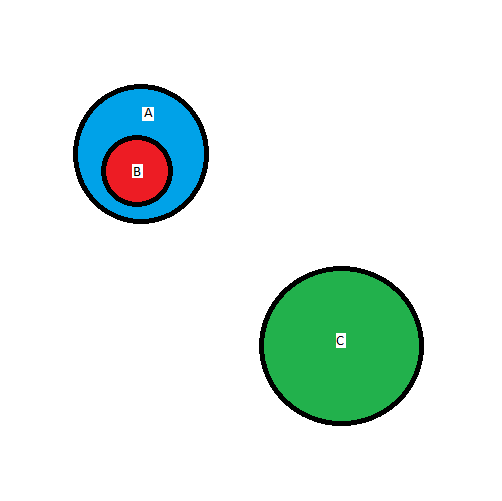 
Tu es sur que ?
Bonjour
Je me permets de suggérer une meilleure formulation
Soit . Alors
et donc
si
.
Si , alors on a
.
Dans tous les cas, on a montré que , et donc que
pierre >> Pour le (b) le même dessin ne suffit pas, je viens de m'en rendre compte, mais on pourrait trouver.
Parcontre pour le a) même si on change ou par et, la conclusion n'est pas bonne, il faut faire une disjonction comme Jalex le montre 